Em cần phần nào nhỉ .

A = \(\dfrac{5}{1.6}\)+\(\dfrac{5}{6.11}\)+\(\dfrac{5}{11.16}\)+\(\dfrac{5}{16.21}\)+...+\(\dfrac{5}{101.106}\)

A = \(\dfrac{1}{1}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{101}-\dfrac{1}{106}\)

A = \(\dfrac{1}{1}\) - \(\dfrac{1}{106}\)

A = \(\dfrac{105}{106}\)

B = \(\dfrac{3}{1.4}\) +\(\dfrac{3}{4.7}\)+\(\dfrac{3}{7.10}\)+...+\(\dfrac{3}{97.100}\)

B = \(\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\)

B = \(\dfrac{1}{1}\) - \(\dfrac{1}{100}\)

B = \(\dfrac{99}{100}\)

C = \(\dfrac{1}{2.7}+\dfrac{1}{7.12}\) + \(\dfrac{1}{12.17}\)+...+ \(\dfrac{1}{97.102}\)

C= \(\dfrac{1}{5}\) \(\times\)( \(\dfrac{5}{2.7}+\dfrac{5}{7.12}+\dfrac{5}{12.17}+...+\dfrac{5}{97.102}\))

C = \(\dfrac{1}{5}\)\(\times\)(\(\dfrac{1}{2}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{12}\) + \(\dfrac{1}{12}\) - \(\dfrac{1}{17}\)+...+ \(\dfrac{1}{97}\) - \(\dfrac{1}{102}\))

C = \(\dfrac{1}{5}\) \(\times\)( \(\dfrac{1}{2}\) - \(\dfrac{1}{102}\))

C = \(\dfrac{1}{5}\) \(\times\) \(\dfrac{25}{51}\)

C = \(\dfrac{5}{51}\) 

D = \(\dfrac{1}{2}\) +   \(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + \(\dfrac{1}{30}\) + \(\dfrac{1}{42}\) + \(\dfrac{1}{56}\) + \(\dfrac{1}{72}\)

D = \(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + \(\dfrac{1}{5.6}\) + \(\dfrac{1}{6.7}\)+\(\dfrac{1}{7.8}\)+ \(\dfrac{1}{8.9}\)

D = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)+\(\dfrac{1}{2}\)-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-\(\dfrac{1}{6}\)+\(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{8}\)+\(\dfrac{1}{8}\)-\(\dfrac{1}{9}\)

D = \(\dfrac{1}{1}\) - \(\dfrac{1}{9}\)

D = \(\dfrac{8}{9}\)

E = \(\dfrac{3}{2.4}\)+\(\dfrac{3}{4.6}\)+\(\dfrac{3}{6.8}\)+...+\(\dfrac{3}{98.100}\)

E = \(\dfrac{3}{2}\) \(\times\) ( \(\dfrac{2}{2.4}\) + \(\dfrac{2}{4.6}\)+ \(\dfrac{2}{6.8}\)+...+\(\dfrac{2}{98.100}\))

E = \(\dfrac{3}{2}\)\(\times\)( \(\dfrac{1}{2}\) - \(\dfrac{1}{4}\)+ \(\dfrac{1}{4}\) - \(\dfrac{1}{6}\)+\(\dfrac{1}{6}\)-\(\dfrac{1}{8}\)+...+\(\dfrac{1}{98}\) - \(\dfrac{1}{100}\))

E = \(\dfrac{3}{2}\) \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{100}\))

E = \(\dfrac{3}{2}\) \(\times\) \(\dfrac{49}{100}\)

E = \(\dfrac{147}{200}\)

Muốn hoàn thành cv trong `1` ngày, cần :

       \(2\times10=20\) (người)

Vậy muốn hoàn thành cv trong `5` ngày, cần :

       \(20:5=4\) (người)

Bài 37:

a) A = \(\left\{T;R;Ư;Ơ;N;G;Q;U;A\right\}\)

b) B= \(\left\{H;O;C;S;I;N;T;A;E\right\}\)

Bài 38: ( mình viết 2 cách là theo thứ tự nhé ) 

a) A = \(\left\{0;1;2;3;4\right\}\)

    A = \(\left\{x\in N|x< 5\right\}\)

b) M = \(\left\{8;9;10;...;15;16\right\}\)

    M = \(\left\{x\in N|7< x< 17\right\}\)

c) N = \(\left\{3;4;5;6;...;13;14\right\}\)

    N = \(\left\{x\in N|3\le x< 15\right\}\)

d) D = \(\varnothing\) ( D thuộc tập hợp rỗng ) 

    D = \(\left\{x\in N|2< x< 3\right\}\)

e) E = \(\left\{5;6\right\}\)

    E = \(\left\{x\in N|5\le x\le6\right\}\)

f ) F = \(\left\{11;12;13;14;15\right\}\)

    F = \(\left\{x\in N|10< x\le15\right\}\)

Bài 39:

a) A = \(\left\{x\in N|99< x\le999\right\}\)

b) B = \(\left\{x\in N|x< 8\right\}\)

c) C = \(\left\{x\in N|10\le x\le99\right\}\)

d) D = \(\left\{x\in N|0< x< 5\right\}\)

   Chúc bạn học tốt

30km/1,5h = 20km/h

  A       =        \(\dfrac{1}{3}\) + \(\dfrac{2}{3^2}\) + \(\dfrac{3}{3^3}\)+.........+\(\dfrac{100}{3^{100}}\)

3A       = 1 + \(\dfrac{2}{3}\) + \(\dfrac{3}{3^2}\) + \(\dfrac{4}{3^3}\)+...+\(\dfrac{100}{3^{99}}\)

3A - A  = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+...+\(\dfrac{1}{3^{99}}\)- \(\dfrac{100}{3^{100}}\)

2A       = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+...+ \(\dfrac{1}{3^{99}}\) - \(\dfrac{100}{3^{100}}\)

 A        = ( 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+...+ \(\dfrac{1}{3^{99}}\) - \(\dfrac{100}{3^{100}}\)) : 2

Đặt B  =       1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\)+ ........  + \(\dfrac{1}{3^{99}}\) 

     3B = 3 + 1 + \(\dfrac{1}{3}\)  + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\) +...+\(\dfrac{1}{3^{98}}\)

3B - B = 3  - \(\dfrac{1}{3^{99}}\) 

     2B = 3 - \(\dfrac{1}{3^{99}}\)

       B = (3 - \(\dfrac{1}{3^{99}}\)): 2 =\(\dfrac{3}{2}\) - \(\dfrac{1}{3^{99}.2}\)

      A = ( \(\dfrac{3}{2}\) - \(\dfrac{1}{2.3^{99}}\) - \(\dfrac{100}{3^{100}}\)) : 2

      A =  \(\dfrac{3}{4}\) - \(\dfrac{1}{4.3^{99}}\) - \(\dfrac{50}{3^{100}}\) < \(\dfrac{3}{4}\) ( đpcm)

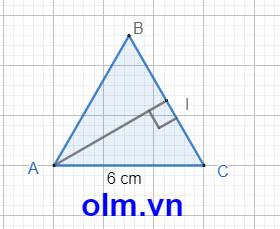
     IC = \(\dfrac{1}{2}\)BC (vì trong tam giác đều đường cao cũng là trung tuyến, đường trung trực, đường phân giác của tam giác đó).

    IC = 6 \(\times\) \(\dfrac{1}{2}\) = 3 (cm)

   Xét \(\Delta\)AIC  vuông tại C nên theo pytago ta có:

      AI² = AC² - IC² = 6² - 3² = 27 (cm)

     AI = \(\sqrt{27}\) = 3\(\sqrt{3}\)(cm)

Chọn A. 3\(\sqrt{3}\)cm

Số đo góc nào bạn?

a) \(\dfrac{8,5-8,2}{16}=\dfrac{0,3}{16}=\dfrac{0,3\cdot10}{16\cdot10}=\dfrac{3}{160}\)

b) \(\dfrac{17\cdot5-17}{3-20}=\dfrac{17\cdot\left(5-1\right)}{-17}=\dfrac{1\cdot4}{-1}=-4\)

a)

\(\dfrac{8\cdot5-8\cdot2}{16}=\dfrac{8\left(5-2\right)}{16}=\dfrac{3}{2}\)

b)

\(\dfrac{17\cdot5-17}{3-20}=\dfrac{17\left(5-1\right)}{-17}=\dfrac{4}{-1}=-4\)

Tranh do học sinh được đồ họa bằng máy tính thì có được tham gia không cô?

Khuyến khích các em sáng tạo không giới hạn, nên các em có thể vẽ tranh bằng đồ họa máy tính nhé.

a. \(\dfrac{8,5-8,2}{16}=\dfrac{0,3}{16}=\dfrac{3}{160}\)

b. \(\dfrac{2\cdot14}{7\cdot8}=\dfrac{1\cdot2}{1\cdot4}=\dfrac{2}{4}=\dfrac{1}{2}\)

c. \(\dfrac{11\cdot4-11}{2-13}=\dfrac{11\left(4-1\right)}{-11}=\dfrac{1\cdot3}{-1}=-3\)

d. \(\dfrac{49+7\cdot49}{49}=\dfrac{49\cdot\left(1+7\right)}{49}=\dfrac{8}{1}=8\)