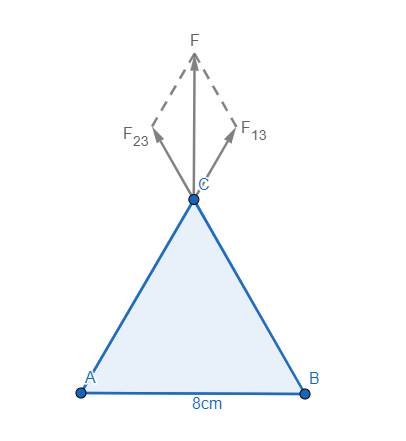
a) Ta có \(F_{13}=\dfrac{k\left|q_1q_3\right|}{AC^2}\) \(=\dfrac{9.10^9\left|6.10^{-6}.4.10^{-6}\right|}{\left(0,08\right)^2}\) \(=33,75\left(N\right)\)

Đồng thời \(F_{13}=F_{23}\) do \(q_1=q_2\)

\(\Rightarrow F=\sqrt{F_{13}^2+F_{23}^2+2F_{13}F_{23}\cos\left(\overrightarrow{F_{13}},\overrightarrow{F_{23}}\right)}\)

\(=\sqrt{33,75^2+33,75^2+2.33,75.33,75\cos60^o}\)

\(\approx58,46\left(N\right)\)

 Vậy vector lực điện do 2 điện tích q₁, q₂ tác dụng lên q₃ là một vector có giá trùng với đường trung trực của AB và có độ lớn khoảng \(58,46N\)

Hiện tượng điện tích dương chuyển động từ nơi có điện tích cao hơn đến nơi có điện tích thấp hơn được giải thích bằng lý thuyết điện trường.

Theo lý thuyết điện trường Coulomb, điện tích dương và điện tích âm tạo ra một lực tương tác gọi là lực điện. Lực điện giữa hai điện tích có magnitutde tỉ lệ thuận với tích của chúng và nghịch với bình phương khoảng cách giữa chúng. Theo công thức Coulomb, lực điện được tính bằng:

F = k * (q1 * q2) / r^2

Trong đó:

- F là lực điện tác động giữa hai điện tích q1 và q2,

- k là hằng số điện trường Coulomb,

- r là khoảng cách giữa hai điện tích.

Do tích có dấu, khi hai điện tích khác dấu (một âm và một dương) thì lực điện sẽ có hướng từ điện tích dương đến điện tích âm. Tương tự, khi hai điện tích cùng dấu (cả hai dương hoặc cả hai âm) thì lực điện sẽ có hướng từ điện tích cao hơn (có magnitutde lớn hơn) đến điện tích thấp hơn (có magnitutde nhỏ hơn). Điều này giải thích vì sao trong điện trường, điện tích dương chuyển động từ nơi có điện tích cao hơn đến nơi có điện tích thấp hơn.

Điện trường có thể được hình dung như một "địa hình" điện mà điện tích dương di chuyển theo. Tuy nhiên, cần lưu ý rằng điện trường không chỉ phụ thuộc vào điện tích mà còn phụ thuộc vào cả tính chất của môi trường và các yếu tố khác.

\(MA=6cm;MB=AB-MA=20-6=14cm\)

\(AM\perp MC\Rightarrow AC=\sqrt{AM^2+MC^2}=\sqrt{6^2+8^2}=10cm\)

\(BM\perp MC\Rightarrow BC=\sqrt{BM^2+MC^2}=\sqrt{14^2+8^2}=2\sqrt{65}cm\)

Xét một điểm N bất kì trên CM ta có: \(d_2-d_1=k\lambda\)

Hai nguồn dao động cùng pha:

\(\Rightarrow\left\{{}\begin{matrix}d_2-d_1=\left(k+0,5\right)\lambda\\BC-AC\le k\lambda\le BM-AM\end{matrix}\right.\)

\(\Rightarrow2\sqrt{65}-10\le k+0,5\le14-6\Rightarrow5,62\le k\le7,5\)

\(\Rightarrow k=\left\{6,5;7,5\right\}\)

Vậy có hai điểm cực tiểu trên CD.

Mình gửi bạn cả công thức và bài làm nhé.