tìm gtnn của biểu thức B=(x+2y)^3-(x-y)(x^2-xy+4y^2)-y(3y+2x)^2-y(2x^2-y+2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(x^8-3x^4+3x^2-1-x^8+1=0\Leftrightarrow-3x^2\left(x^2-1\right)=0\Leftrightarrow x=0;x=1;x=-1\)
b, \(x^3-6x^2+12x-8-x^3+27+6x^2+12x+6=49\)
\(\Leftrightarrow24x-24=0\Leftrightarrow x=1\)
c, \(8x^3-27-98=0\Leftrightarrow8x^3-125=0\Leftrightarrow\left(2x-5\right)\left(4x^2+10x+25\ne0\right)=0\Leftrightarrow x=\dfrac{5}{2}\)
d, \(27-\dfrac{1}{8}x^3-19=0\Leftrightarrow8-\dfrac{1}{8}x^3=0\Leftrightarrow\left(2-\dfrac{1}{2}x\right)\left(4+x+\dfrac{1}{4}x^2\ne0\right)=0\Leftrightarrow x=4\)




a/
\(a^2+b^2=ab+ba=2ab\)
\(\Rightarrow\left(a-b\right)^2=0\Rightarrow a-b=0\Rightarrow a=b\)
b/ Ta có
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Mà \(a^2+b^2+c^2=ab+bc+ca\)
\(\Rightarrow a^3+b^3+c^3=3abc\)
Theo AM-GM có
\(\dfrac{a^3+b^3+c^3}{3}\ge\sqrt[3]{a^3b^3c^3}=abc\)
\(\Rightarrow a^3+b^3+c^3\ge3abc\) Dấu = xảy ra khi
\(a^3=b^3=c^3\Rightarrow a=b=c\)


`2x^3-16x^2+18x=0`
`<=>2x(x^2-8x+9)=0`
`<=>2x(x^2-8x+16-7)=0`
`<=>2x[(x-4)^2-7]=0`
`<=>` $\left[\begin{matrix} 2x=0\\ (x-4)^2-7=0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=0\\ (x-4)^2=7\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=0\\ x-4=\pm \sqrt{7}\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=0\\ x=4 \pm \sqrt{7}\end{matrix}\right.$
Vậy `S={0;4+-\sqrt{7}}`
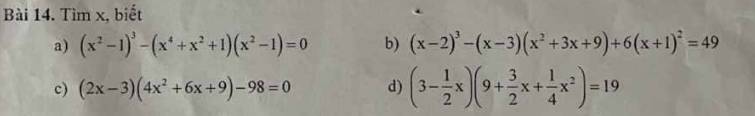
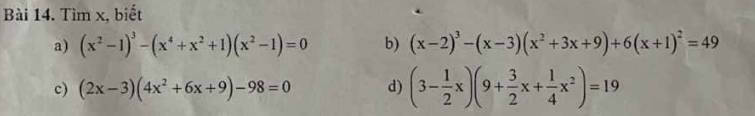
 mn giúp em với ạ
mn giúp em với ạ