 mng giúp e vs ạ
mng giúp e vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2}{1\cdot6}+\dfrac{2}{11\cdot16}+...+\dfrac{2}{x\left(x+5\right)}=\dfrac{41}{103}\\ =>\dfrac{2}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{x\left(x+5\right)}\right)=\dfrac{41}{103}\\ =>1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{x}-\dfrac{1}{x+5}=\dfrac{41}{103}:\dfrac{2}{5}=\dfrac{205}{206}\\ =>1-\dfrac{1}{x+5}=\dfrac{205}{206}\\ =>1-\dfrac{1}{x+5}=1-\dfrac{1}{206}\\ =>\dfrac{1}{x+5}=\dfrac{1}{206}\\ =>x+5=206\\ =>x=206-5=201\)

a: ta có: \(\widehat{MAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AM//BC
ta có: \(\widehat{CAN}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//BC
Ta có: AM//BC
NA//BC
mà AM,AN có điểm chung là A
nên M,A,N thẳng hàng
b: Vì M,A,N thẳng hàng nên \(\widehat{MAB}+\widehat{BAC}+\widehat{CAN}=180^0\)
=>\(\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)


\(\left(x+2\right)^2+2\left(y-3\right)^2< 4\)
mà x,y nguyên
nên \(\left[\left(x+2\right)^2;2\left(y-3\right)^2\right]\in\left\{\left(1;2\right);\left(0;2\right)\right\}\)
=>\(\left(x+2;y-3\right)\in\left\{\left(1;1\right);\left(1;-1\right);\left(-1;1\right);\left(-1;-1\right);\left(0;1\right);\left(0;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-1;4\right);\left(-1;2\right);\left(-3;4\right);\left(-3;2\right);\left(-2;4\right);\left(-2;2\right)\right\}\)

a: Ta có: xx'\(\perp\)AB
yy'\(\perp\)AB
Do đó: xx'//yy'
b: xx'//y'y
=>\(\widehat{ADC}=\widehat{C_1}\)(hai góc so le trong)
=>\(\widehat{C_1}=74^0\)
c: DE là phân giác của góc CDF
=>\(\widehat{FDE}=\dfrac{\widehat{FDC}}{2}=\dfrac{106^0}{2}=53^0\)
Xét ΔDEF có \(\widehat{x'FE}\) là góc ngoài tại F
nên \(\widehat{x'FE}=\widehat{FED}+\widehat{FDE}=70^0+53^0=123^0\)

\(\left(x+5\right)^2-4x^2\\=\left(x+5\right)^2-\left(2x\right)^2\\ =\left[\left(x+5\right)-2x\right]\left[\left(x+5\right)+2x\right]\\ =\left(x+5-2x\right)\left(x+5+2x\right)\\ =\left(-x+5\right)\left(3x+5\right)\)

`a` là số tự nhiên không chia hết cho `3` nên a có dạng:
`a = 3k + 1` hoặc `a = 3k + 2`
(`k` thuộc `N`*)
Mà a là số tự nhiên lẻ `=> a^2` là số tự nhiên lẻ `=> a^2 - 1` là số chẵn
`=> a^2 ⋮ 2`
Để `a^2 - 1 ⋮ 6` thì `a^2 - 1 ⋮ 3` (Vì `UCLN(2;3) = 1`)
- Xét `a = 3k + 1`
`=> a^2 -1 = (3k+1)^2 -1= 9k^2 + 6k + 1 - 1= 9k^2 + 6k^2 ⋮ 3` (Thỏa mãn)
- Xét `a = 3k + 2`
`=> a^2 -1 = (3k+2)^2 -1 = 9k^2 + 12k + 4 - 1= 9k^2 + 12k^2 + 3 ⋮ 3` (Thỏa mãn)
Vậy ...
Chứng minh: \(\dfrac{3}{1^2\cdot2^2}\)+\(\dfrac{5}{2^2\cdot3^2}\)+...+\(\dfrac{19}{9^2\cdot10^2}\)<1

\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}\)
= \(\dfrac{3}{1.4.}+\dfrac{5}{4.9}+...+\dfrac{19}{81.100}\)
= \(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}+\dfrac{1}{100}\)
= \(1-\dfrac{1}{100}< 1\) (đpcm)
--------------------------------
Cho các số: a;b;c thuộc `N`; `c,b` khác `0` ta luôn có:
Nếu: `c-b = a` thì:
\(\dfrac{a}{b.c}=\dfrac{1}{b}-\dfrac{1}{c}\)
Ta có:
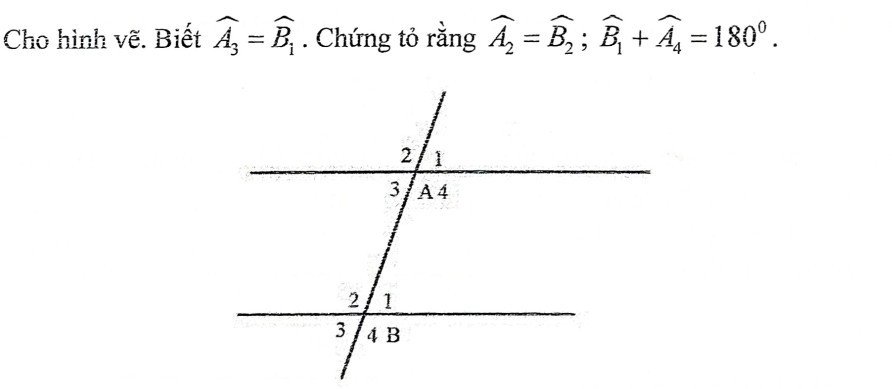
∠A₃ = ∠B₁ (gt)
Mà ∠A₃ và ∠B₁ là hai góc so le trong
⇒ a // b
⇒ ∠A₂ = ∠B₂ (đồng vị)
Do ∠A₃ + ∠A₄ = 180⁰ (kề bù)
Mà ∠A₃ = ∠B₁ (gt)
⇒ ∠B₁ + ∠A₄ = 180⁰