chứng minh (a+b)3=a3+3a2b+b3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{24}{21}\cdot\dfrac{9}{8}=\dfrac{8}{7}\cdot\dfrac{9}{8}=\dfrac{9}{7}\)

Hiệu số phần bằng nhau là 4-1=3(phần)
Số bé là 120:3x1=40
Số lớn là 40+120=160

Nếu xóa chữ số 0 ở hàng đơn vị của số thứ nhất thì ta được số thứ hai nên số thứ nhất=10 lần số thứ hai
9 lần số thứ hai là số thứ nhất-số thứ hai=459
=>Số thứ hai là 459:9=51
Số thứ nhất là 51x10=510
Nếu xóa chữ số 0 ở hàng đơn vị của số thứ nhất thì ta được số thứ hai nên số thứ nhất=10 lần số thứ hai
9 lần số thứ hai là số thứ nhất-số thứ hai=459
=>Số thứ hai là 459:9=51
Số thứ nhất là 51x10=510

Số lượng số hạng là:
(299 - 1) : 2 + 1 = 150 (số hạng)
Tổng của dãy số là:
(299 + 1) x 150 : 2 = 22500

\(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+.\dfrac{x-64}{9}=10\\ \Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\\ \Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\\ \Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\\ \Leftrightarrow x-100=0\\ \Leftrightarrow x=100\)
\(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\\\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\\ \left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0 \\ \dfrac{x-85-15}{15}+\dfrac{x-74-26}{13}+\dfrac{x-67-33}{11}+\dfrac{x-64-36}{9}=0\\ \dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\\ \left(x-100\right)\cdot\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)
Vì \(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\ne0\)

Cảm ơn Trần Khánh Phương nhé
Bạn có thể giải cả bài cho tớ được khum!

\(A=3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\\ 3A=3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\\ 3A+A=\left(3^{101}-3^{100}+3^{99}-3^{98}+...+3^3-3^2+3\right)+\left(3^{100}-3^{99}+3^{98}-3^{97}+...+3^2-3+1\right)\\ 4A=3^{101}+\left(3^{100}-3^{100}\right)+\left(3^{99}-3^{99}\right)+...+\left(3^2-3^2\right)+\left(3-3\right)-1\\ 4A=3^{101}-1\\ A=\dfrac{3^{101}-1}{4}\)
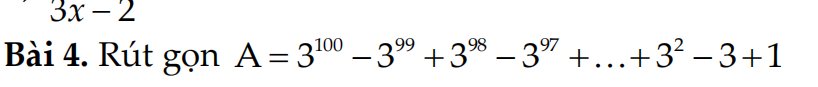
Sửa đề: Chứng minh \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
Bài làm:
\(VT=\left(a+b\right)^3=\left(a+b\right)\left(a+b\right)\left(a+b\right)\\ =\left(a^2+ab+ab+b^2\right)\left(a+b\right)\\ =\left(a^2+2ab+b^2\right)\left(a+b\right)\\ =a^3+2a^2b+ab^2+a^2b+2ab^2+b^3\\ =a^3+3a^2b+3ab^2+b^3=VP\left(DPCM\right)\)