lớp 6a có tổng số học sinh là 35 em biết 2/7 số học sinh trong lớp tham gia câu lạc bộ toán 3/5 số học sinh trong lớp tham gia câu lạc bộ bóng đá số học sinh còn lại không tham gia câu lạc bộ nào tính số học sinh không tham gia câu lạc bộ của lớp 6a. Giup với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d = ƯCLN(2n - 3; n - 2)
⇒ (2n - 3) ⋮ d và (n - 2) ⋮ d
*) (n - 2) ⋮ d
⇒ 2(n - 2) ⋮ d
⇒ (2n - 4) ⋮ d
Mà (2n - 3) ⋮ d
⇒ [2n - 3 - (2n - 4)] ⋮ d
⇒ (2n - 3 - 2n + 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy A là phân số tối giản
Chỉ có A=\(\dfrac{2n-3}{n-2}\) thì mới có điều kiện n≠2 bạn nhé.

Ngày thứ nhất bạn An đã đọc số trang là:
120x\(\dfrac{3}{8}\) = 45 (trang)
Ngày thứ hai bạn An đã đọc số trang là:
120x\(\dfrac{2}{5}\) = 48 (trang)
Ngày thứ ba bạn An đã đọc số trang là:
120-45-48=27 (trang)
Đáp số: Ngày 1: 45 trang
Ngày 2: 48 trang
Ngày 3: 27 trang
Ngày thứ nhất An đọc được số trang của cuốn truyện là:
120 * (3/8) = 45 trang
Ngày thứ hai An đọc được số trang của cuốn truyện là:
120 * (2/5) = 48 trang
Ngày thứ ba An đọc được số trang là:
120 - 45 - 48 = 27 trang
Vậy số trang mà bạn An đã đọc trong mỗi ngày lần lượt là: 45 trang, 48 trang, 27 trang.

\(2\cdot3^{x-1}+\left(-3\right)^2=3^3\)
=>\(2\cdot3^{x-1}+9=27\)
=>\(2\cdot3^{x-1}=18\)
=>\(3^{x-1}=9\)
=>x-1=2
=>x=3

Số điểm còn lại là n-3(đường)
TH1: Chọn 1 điểm trong 3 điểm thẳng hàng, chọn 1 điểm trong n-3 điểm còn lại
=>Có \(3\cdot\left(n-3\right)=3n-9\left(đường\right)\)
TH2: Chọn 2 trong n-3 điểm còn lại
=>Có \(C^2_{n-3}=\dfrac{\left(n-3\right)!}{\left(n-3-2\right)!\cdot2!}=\dfrac{\left(n-3\right)\left(n-4\right)}{2}\left(đường\right)\)
TH3: Vẽ 1 đường thẳng đi qua 3 điểm thẳng hàng
=>Có 1 đường
Tổng số đường thẳng vẽ được là:
\(3n-9+1+\dfrac{\left(n-3\right)\left(n-4\right)}{2}=\dfrac{2\left(3n-8\right)+n^2-7n+12}{2}\)
\(=\dfrac{6n-16+n^2-7n+12}{2}=\dfrac{n^2+n-4}{2}\left(đường\right)\)

Số đường thẳng vẽ được là:
\(C^2_n=\dfrac{n!}{\left(n-2\right)!\cdot2!}=\dfrac{n\left(n-1\right)}{2}\left(đường\right)\)
Giải:
Cứ 1 điểm sẽ tạo với (n - 1) điểm còn lại n - 1 đường thẳng
Với n điểm sẽ tạo được: (n - 1).n đường thẳng
Theo cách tính trên mỗi đường thẳng được tính hai lần. Thực tế số đường thẳng tạo được là:
(n - 1). n : 2
Kết luận:

a; 13.4.47 + 53.166 - 53.114
= 13.4.57 + 53.(166 - 114)
= 13.4.57 + 53.52
= 52.47 + 53.52
= 52.(47 + 53)
= 52.100
= 5200
b; 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + ... + 993 + 994 - 995 - 996 + 997 + 998
Xét dãy số trên có 998 số hạng vì 998 : 4 = 249 dư 2 nên khi nhóm 4 số hạng của tổng trên thành một nhóm thì
B= (1 +2 - 3 -4) + (5 + 6 - 7 - 8) +...+ (993 + 994 - 995 - 996)+ 997+998
B = - 4 + - 4 + ... + -4 + 997 + 998
B = -4 x 249 + 997 + 998
B = -996 + 997 + 998
B = 1 + 998
B = 999

S = \(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + ... + \(\dfrac{1}{98.99}\) + \(\dfrac{1}{99.100}\)
S = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + ... + \(\dfrac{1}{98}\) - \(\dfrac{1}{99}\) + \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
S = 1 - \(\dfrac{1}{100}\) < 1
Vậy S < 1

Giải:
2 giờ 30 phút = 2,5 giờ
Quãng đường AB dài là: 60,8 x 2,5 = 152 (km)
Thời gian ô tô đi từ B về A là:
152 : 50 = 3,04 (giờ)
3,04 giờ = 3 giờ 2phút 24 giây
Kết luận:..
Q
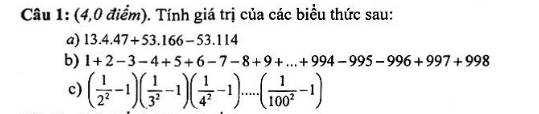
Số học sinh tham gia câu lạc bộ Toán là \(35\cdot\dfrac{2}{7}=10\left(bạn\right)\)
Số học sinh tham gia câu lạc bộ bóng đá là \(35\cdot\dfrac{3}{5}=21\left(bạn\right)\)
Số bạn không tham gia câu lạc bộ nào là:
35-10-21=4(bạn)