31x+50= 30 căn ( x-3) + 48 căn ( x+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Đặt \(A=-x^2-2y^2+2xy-4x+2y-12\)
\(A=-\left(x^2-2xy+y^2\right)-4\left(x-y\right)-y^2-2y-1-11\)
\(=-\left(x-y\right)^2-4\left(x-y\right)-4-\left(y^2+2y+1\right)-7\)
\(=-\left[\left(x-y\right)^2+4\left(x-y\right)+4\right]-\left(y+1\right)^2-7\)
\(=-\left(x-y+2\right)^2-\left(y+1\right)^2-7\)
Do \(\left\{{}\begin{matrix}-\left(x-y+2\right)^2\le0\\-\left(y+1\right)^2\le0\end{matrix}\right.\) ; \(\forall x;y\)
\(\Rightarrow A\le-7\)
\(A_{max}=-7\) khi \(\left\{{}\begin{matrix}x-y+2=0\\y+1=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-3;-1\right)\)
2.
Đặt \(B=-10x^2-y^2+6xy+10x-2y+2\)
\(=-\left(9x^2-6xy+y^2\right)+2\left(3x-y\right)-x^2+4x-4+6\)
\(=-\left(3x-y\right)^2+2\left(3x-y\right)-1-\left(x^2-4x+4\right)+7\)
\(=-\left[\left(3x-y\right)^2-2\left(3x-y\right)+1\right]-\left(x-2\right)^2+7\)
\(=-\left(3x-y-1\right)^2-\left(x-2\right)^2+7\le7\)
\(B_{max}=7\) khi \(\left\{{}\begin{matrix}3x-y-1=0\\x-2=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(2;5\right)\)


a: Ta có: BA//CD
mà B\(\in AE\)
nên BE//CD
Ta có: BA=CD
BA=BE
Do đó: BE=CD
Xét tứ giác BECD có
BE//CD
BE=CD
Do đó: BECD là hình bình hành
c: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Ta có: BDCE là hình bình hành
=>BD//CE và BD=CE
Ta có:BD=CE
mà BD=2OB và CE=2CI
nên OB=CI
Xét tứ giác BOCI có
BO//CI
BO=CI
Do đó: BOCI là hình bình hành

\(2a^2+b^2+c^2>=2a\left(b+c\right)\)
=>\(\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)>=0\)
=>\(\left(a-b\right)^2+\left(a-c\right)^2>=0\)(luôn đúng)

2024:4=506; 2024:5 dư 4
=>Chữ thứ 2024 là tiếng GIAO, màu vàng
2025:4=506 dư 1; 2025 chia hết cho 5
=>Chữ thứ 2025 là tiếng THONG, màu xanh
2024:4=506; 2024:5 dư 4
Chữ thứ 2024 là tiếng GIAO, màu vàng
2025:4=506 dư 1; 2025 chia hết cho 5
Chữ thứ 2025 là tiếng THONG, màu xanh

2a+3>=2b+4
=>2a+3-4>=2b+4-4
=>2a-1>=2b
mà 2a+1>2a-1(1>-1)
nên 2a+1>2b
\(2a+3\ge2b+4\)
\(\Leftrightarrow2a+1\ge2b+2\)
\(\Rightarrow2a+1>2b\)

\(\left(x+2\right)^2+2\left(y-3\right)^2< 4\)
mà x,y nguyên
nên \(\left[\left(x+2\right)^2;2\left(y-3\right)^2\right]\in\left\{\left(1;2\right);\left(0;2\right)\right\}\)
=>\(\left(x+2;y-3\right)\in\left\{\left(1;1\right);\left(1;-1\right);\left(-1;1\right);\left(-1;-1\right);\left(0;1\right);\left(0;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-1;4\right);\left(-1;2\right);\left(-3;4\right);\left(-3;2\right);\left(-2;4\right);\left(-2;2\right)\right\}\)

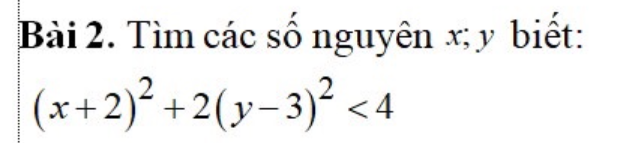
Lần sau em cần gõ đề bài bằng công thức toán học có biểu tượng \(\Sigma\) bên trái màn hình em nhé.