a: \(\dfrac{-1}{4}+\dfrac{3}{6}=\dfrac{-1}{4}+\dfrac{1}{2}=\dfrac{-1+2}{4}=\dfrac{1}{4}\)

b: \(\dfrac{-2}{5}\cdot\dfrac{5}{6}+\dfrac{-2}{5}\cdot\dfrac{1}{6}-2\dfrac{3}{5}\)

\(=\dfrac{-2}{5}\left(\dfrac{5}{6}+\dfrac{1}{6}\right)-\dfrac{13}{5}\)

\(=\dfrac{-2}{5}-\dfrac{13}{5}=-3\)

\(\dfrac{8}{11}\)  x (-5) = \(\dfrac{-40}{11}\)

$-5 \times \frac{8}{11} = -\frac{40}{11} \approx -3,64$

Chọn C

B = (\(\dfrac{1}{4}\) - 1).(\(\dfrac{1}{9}\) - 1).(\(\dfrac{1}{16}\)  - 1)...(\(\dfrac{1}{900}\) - 1)

B = \(\dfrac{-3}{4}\).\(\dfrac{-8}{9}\).\(\dfrac{-15}{16}\)...\(\dfrac{-899}{900}\)

B = \(\dfrac{-1.3}{2.2}\).\(\dfrac{-2.4}{3.3}\).\(\dfrac{-3.5}{4.4}\)...\(\dfrac{-29.31}{30.30}\)

Xét dãy số: 2; 3; 4; ...;30 Dãy số trên có số số hạng là:

(30 - 2): 1 + 1  =  29 

Vậy B là tích của 29 số âm nên B là  một số âm

B =  - \(\dfrac{1}{2}.\dfrac{31}{30}\)

B = - \(\dfrac{31}{60}\)

\(3^{303}=27^n\)

=>\(3^{303}=3^{3n}\)

=>3n=303

=>n=101

3³⁰³ = 27ⁿ

n      = 27 : 3

n      = 9

(kết quả mik tính chưa chắc đúng đâu , mik làm theo khả năng)

Số học sinh giỏi là \(36\cdot\dfrac{1}{9}=4\left(bạn\right)\)

Số học sinh khá là \(4:\dfrac{1}{5}=20\left(bạn\right)\)

Số học sinh trung bình là 36-4-20=12(bạn)

Gọi số học sinh giỏi là $x$, số học sinh khá là $y$, và số học sinh trung bình là $z$.
--> Tổng số học sinh trong lớp là 36, vì vậy $x + y + z = 36$.
--> Số học sinh giỏi bằng 1/9 tổng số cả lớp và bằng 1/5 số học sinh khá, vì vậy $x = \frac{1}{9} \times 36 = 4$ và $x = \frac{1}{5}y$.
Số học sinh khá là $y = 5x = 5 \times 4 = 20$.
Số học sinh trung bình là: $z = 36 - x - y = 36 - 4 - 20 = 12$.
=> Vậy, số học sinh giỏi là 4, số học sinh khá là 20, và số học sinh trung bình là 12.

~~~~~~~~~~~~

Bú j bạn =))??

\(\dfrac{8}{15}=\dfrac{8\cdot6}{15\cdot6}=\dfrac{48}{90}\)

\(\dfrac{-7}{18}=\dfrac{-7\cdot5}{18\cdot5}=\dfrac{-35}{90}\)

\(\dfrac{13}{90}=\dfrac{13\cdot1}{90\cdot1}=\dfrac{13}{90}\)

8/15 = (8×6)/(15×6) = 48/90

-7/18 = (-7×5)/(18×5) = -35/90

13/90 = 13/90

tick nha

a: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2023\cdot2024}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\)

\(=1-\dfrac{1}{2024}=\dfrac{2023}{2024}\)

b: \(B=\dfrac{2}{1\cdot2}+\dfrac{2}{2\cdot3}+...+\dfrac{2}{2023\cdot2024}\)

\(=2\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2023\cdot2024}\right)\)

\(=2\cdot\dfrac{2023}{2024}=\dfrac{2023}{1012}\)

c: \(C=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{101\cdot103}\)

\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{101}-\dfrac{1}{103}\)

\(=1-\dfrac{1}{103}=\dfrac{102}{103}\)

a: Số đoạn thẳng tạo thành là:

\(\dfrac{26\left(26-1\right)}{2}=13\cdot25=325\left(đoạn\right)\)

b: Theo đề, ta có: \(C^2_n=496\)

=>\(\dfrac{n!}{\left(n-2\right)!\cdot2!}=496\)

=>n(n-1)=496*2=992

=>\(n^2-n-992=0\)

=>\(\left[{}\begin{matrix}n=32\left(nhận\right)\\n=-31\left(loại\right)\end{matrix}\right.\)

c: Số điểm còn lại là 26-4=22(điểm)

TH1: Lấy 1 điểm trong 4 điểm thẳng hàng, lấy 1 điểm trong 22 điểm còn lại

=>Có 4*22=88(đường)

TH2: vẽ 1 đường thẳng đi qua 4 điểm thẳng hàng

=>Có 1 đuờng

TH3: Lấy 2 điểm trong 22 điểm còn lại

=>Có \(C^2_{22}=231\left(đường\right)\)

Số đường thẳng là: 231+1+88=320 đường

Lời giải:

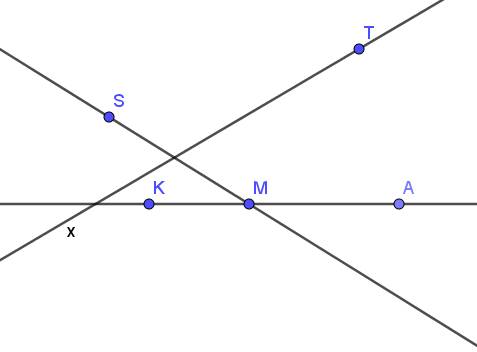
1. Ba điểm thẳng hàng là $K,M,A$ và điểm $M$ nằm giữa $K,A$

2. Hai tia đối nhau: $MK, MA$