Giải phương trình: \(\sin^4+\cos^4-\cos^2+\frac{1}{4\sin^22x}-1=0.\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

NT
1

NM
Nguyễn Minh Quang
Giáo viên
13 tháng 3 2021
ta có bài toán đúng với n=1
giả sử đúng với n=k
xét n=k+1:
\(29^{2\left(k+1\right)}-140\left(k+1\right)-1\)
\(=841.29^{2k}-140k-141=700.29^{2k}+141.\left(29^{2k}-140k-1\right)+19600k\)
mà \(\hept{\begin{cases}700.29^{2k}⋮700\\140\left(29^{2k}-140k-1\right)⋮700\\19600⋮700\end{cases}}\)bài toán đúng với n=k+1
Vậy theo nguyên lý quy nạp ta chứng minh được bài toán

13 tháng 3 2021
d/ \(x^3-x^2-x-5=\left(x+4\right)\sqrt{x+2}\)
\(\Leftrightarrow\left(x-1\right)^3+2\left(x-1\right)^2+2\left(x-1\right)=\left(x+2+2\right)\sqrt{x+2}+2\left(x+2\right)\)
Đặt \(\hept{\begin{cases}x-1=a\\\sqrt{x+2}=b\end{cases}}\)
\(\Rightarrow a^3+2a^2+2a=b^3+2b^2+2b\)
\(\Leftrightarrow a=b\)
Làm nốt
NL
0

G
1
G
1
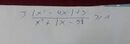
ta có
\(sin^4x+cos^4x-1=-2sin^2xcos^2x\)
vì vậy phương trình \(\Leftrightarrow-2sin^2x.cos^2x+\frac{1}{4sin^22x}=0\Leftrightarrow sin^42x=\frac{1}{2}\Rightarrow sin2x=\pm\frac{1}{\sqrt[4]{2}}\)
\(\Rightarrow\)\(\orbr{\begin{cases}x=\pm\frac{1}{2}arcsin\left(\frac{1}{\sqrt[4]{2}}\right)+k\pi\\x=\frac{\pi}{2}\mp arcsin\left(\frac{1}{\sqrt[4]{2}}\right)+k\pi\end{cases}}\)
Trần Mạnh Q , nếu hôm đấy anh làm sớm 1 h thì hay bt bao ko anh