2(x+1)-1=3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
\(=\sqrt{\sqrt{3^2}+2\sqrt{3}.\sqrt{2}+\sqrt{2^2}}-\sqrt{\sqrt{3^2}-2.\sqrt{3}.\sqrt{2}+\sqrt{2^2}}\)
\(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{3}+\sqrt{2}\right|-\left|\sqrt{3}-\sqrt{2}\right|\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{2}\)

\(3,\dfrac{\sqrt{9+6\sqrt{2}}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3\left(3+2\sqrt{2}\right)}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3}.\sqrt{3+2\sqrt{2}}}{\sqrt{3}}\)
\(=\sqrt{3+2\sqrt{2}}\)
\(=\sqrt{\sqrt{2^2}+2\sqrt{2}+1}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(=\left|\sqrt{2}+1\right|=\sqrt{2}+1\)
\(4,\sqrt{2+\sqrt{3}}:\sqrt{\dfrac{1}{2}}\)
\(=\sqrt{2+\sqrt{3}}:\dfrac{1}{\sqrt{2}}\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{2}\)
\(=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\sqrt{3^2}+2\sqrt{3}+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)}^2\)
\(=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)

Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất tia phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$
$\Rightarrow BD=20:(3+4).3=\frac{60}{7}$ (cm)
Theo hệ thức lượng của tam giác vuông:
$HB=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2$ (cm)
$CH=BC-HB=20-7,2=12,8$ (cm)
$HD=BD-BH=\frac{60}{7}-7,2=\frac{48}{35}$ (cm)

Để tính AB và AC, ta sẽ sử dụng định lý Pythagoras trong tam giác vuông.
Với ∆ABC vuông tại A và BD là phân giác của góc B, ta có:
BD/BC = 3/4
Vì BD/BC = 3/4, ta có thể xác định giá trị của BD và CD:
BD = (3/4) * BC = (3/4) * 20cm = 15cm CD = BC - BD = 20cm - 15cm = 5cm
Với AB > AC, ta có thể gọi AB = x và AC = y (với x > y).
Áp dụng định lý Pythagoras trong tam giác vuông ABC, ta có:
AB^2 = AC^2 + BC^2
x^2 = y^2 + 20^2
Ta cũng biết rằng BD là phân giác của góc B, do đó:
AD = DC = 5cm
Áp dụng định lý Pythagoras trong tam giác vuông ABD, ta có:
AB^2 = AD^2 + BD^2
x^2 = 5^2 + 15^2
x^2 = 25 + 225
x^2 = 250
Từ phương trình trên, ta có x = √250 = 5√10
Do đó, AB = 5√10 cm.
Tiếp theo, ta sẽ tính giá trị của y (AC).
Áp dụng định lý Pythagoras trong tam giác vuông ACD, ta có:
AC^2 = AD^2 + CD^2
y^2 = 5^2 + 5^2
y^2 = 25 + 25
y^2 = 50
Từ phương trình trên, ta có y = √50 = 5√2
Do đó, AC = 5√2 cm.
Tóm lại, AB = 5√10 cm và AC = 5√2 cm.

Lời giải:
Theo tính chất tia phân giác:
$\frac{AB}{AC}=\frac{BD}{DC}=\frac{75}{100}=\frac{3}{4}(1)$
$BC=BD+CD=75+100=175$
Theo định lý Pitago:
$AB^2+AC^2=BC^2=175^2(2)$
Từ $(1); (2)\Rightarrow AB=105; AC=140$ (cm)
$BH=\frac{AB^2}{BC}=\frac{105^2}{175}=63$ (cm) - theo hệ thức lượng trong tam giác vuông
$CH=BC-BH=175-63=112$ (cm)
$AH=\sqrt{AB^2-BH^2}=\sqrt{105^2-63^2}=84$ (cm)
$HD=BD-BH=75-63=12$ (cm)
$AD=\sqrt{AH^2+DH^2}=\sqrt{84^2+12^2}=60\sqrt{2}$ (cm)

Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
Áp dụng tính chất tia phân giác:
$\frac{AE}{EC}=\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}$
Mà: $AE+EC=AC=8$
$\Rightarrow EC=8:(3+5).5=5$ (cm)
$AE=AC-EC=8-5=3$ (cm)
$EB=\sqrt{AB^2+AE^2}=\sqrt{6^2+3^2}=3\sqrt{5}$ (cm)

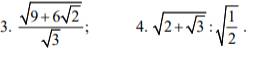 áp dụng quy tắc chia căn bậc hai, hãy tính
áp dụng quy tắc chia căn bậc hai, hãy tính
\(2\left(x+1\right)-1=3\)
\(\Leftrightarrow2\left(x+1\right)=3+1\)
\(\Leftrightarrow2\left(x+1\right)=4\)
\(\Leftrightarrow x+1=4:2\)
\(\Leftrightarrow x+1=2\)
\(\Leftrightarrow x=2-1\)
\(\Leftrightarrow x=1\)