Căn 25/4 - căn 49/16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
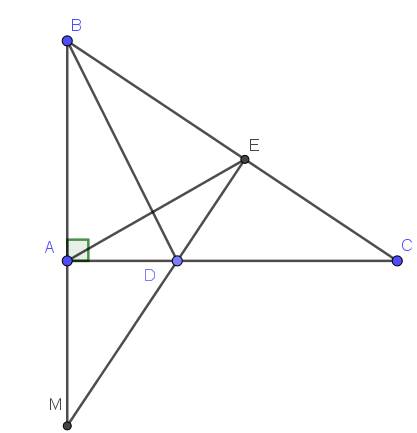
a. Xét tam giác $ABD$ và $EBD$ có:
$AB=EB$
$BD$ chung
$\widehat{ABD}=\widehat{EBD}$ (do $BD$ là phân giác $\widehat{B}$)
$\Rightarrow \triangle ABD=\triangle EBD$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra:
$AD=DE$
$\widehat{BED}=\widehat{BAD}=90^0$
$\Rightarrow DE\perp BC$
$\Rightarrow \widehat{DEC}=90^0$
Xét tam giác $ADM$ và $EDC$ có:
$AD=ED$ (cmt)
$\widehat{ADM}=\widehat{EDC}$ (đối đỉnh)
$\widehat{DAM}=\widehat{DEC}=90^0$
$\Rightarrow \triangle ADM=\triangle EDC$ (g.c.g)
$\Rightarrow AM=EC$
c.
Từ tam giác bằng nhau phần b suy ra:
$\widehat{M_1}=\widehat{C_1}$
$DM=DC$
Mà $DE=AD$
$\Rightarrow DM+DE=DC+AD$
$\Rightarrow ME=AC$
Xét tam giác $AEM$ và $EAC$ có:
$AM=EC$ (cmt)
$EM=AC$ (cmt)
$\widehat{M_1}=\widehat{C_1}$ (cmt)
$\Rightarrow \triangle AEM=\triangle EAC$ (c.g.c)
$\Rightarrow \widehat{EAM}=\widehat{AEC}$

7\(x\) - 2y = 15
y =( 7\(x\) - 15) : 2
⇒ 7\(x\) - 15 ⋮ 2
⇒ \(x\) - 1 ⋮ 2
⇒ \(x\) = 2k + 1; k \(\in\) N
Vì y là số tự nhiên nên 7\(x\) - 15 ≥ 0 ⇒ \(x\) ≥ \(\dfrac{15}{7}\)
⇒ 2k + 1 ≥ \(\dfrac{15}{7}\)
k ≥ (\(\dfrac{15}{7}\) - 1 ) : 2
k ≥ \(\dfrac{8}{14}\) ⇒ k ≥ 1;
⇒ \(x\) = 2k + 1; k ϵ N*
y = \(\dfrac{7.\left(2k+1\right)-15}{2}\)
y = 7k - 4
Vậy câc cặp số tự nhiên \(x;y\) thỏa mãn đề bài là
(\(x;y\)) = (2k+1; 7k - 4); k \(\in\)N*

\(\left(\dfrac{-3}{4}\right)^2.\left(\dfrac{-6}{9}\right)^2\)
\(=\left(\dfrac{-3}{4}.\dfrac{-6}{9}\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
*Công thức: \(a^m.b^m=\left(a.b\right)^m\)
\(#Thitottt:3\)

(-4)2.(-\(\dfrac{3}{2}\))2
= (- 4. (-\(\dfrac{3}{2}\)))2
= 62
= 36

\(\sqrt{\dfrac{25}{4}}-\sqrt{\dfrac{49}{16}}=\dfrac{5}{2}-\dfrac{7}{4}=\dfrac{10}{4}-\dfrac{7}{4}=\dfrac{3}{4}\)
căn 25/4-căn 49/16=căn(5/2)mũ 2-căn(7/4)mũ 2=5/2-7/4=3/4