write a paragraph (50 or more) about the reasons why students join different community activities
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-acy}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-acy+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{y}{b}=\frac{z}{c}; \frac{z}{c}=\frac{x}{a}$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$

\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{b+c+c+a+a+b}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{b+c}{a}=\dfrac{c+a}{b}=\dfrac{a+b}{c}=2\)
\(\Rightarrow A=2020-2+2-2=2018\)
write a paragraph (50 or more) about the reasons why students join different community activities

vì \(x\) và y là hai đại lượng tỉ lệ thuận nên \(x\) = ky
Thay \(x\) = 3; y = -9 vào biểu thức: \(x\) = ky ta có:
3 = k.(-9) ⇒ k = 3 : (-9) = - \(\dfrac{1}{3}\)
⇒ \(x\) = - \(\dfrac{1}{3}\)y
với \(x\) = -1,5 ta có: -1,5 = - \(\dfrac{1}{3}\)y ⇒ y = -1,5.(-3) = 4,5

Lời giải:
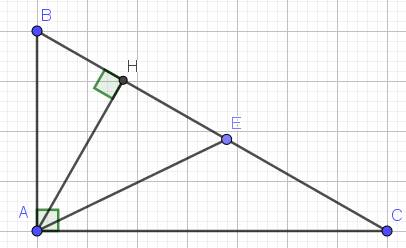
Ta có: $\widehat{BAE}=\widehat{BAC}-\widehat{EAC}$
$=90^0-\frac{1}{2}\widehat{HAC}(1)$
$\widehat{AEB}=\widehat{EAC}+\widehat{ECA}$
$=\frac{1}{2}\widehat{HAC}+(90^0-\widehat{HAC})$
$=90^0-\frac{1}{2}\widehat{HAC}(2)$
Từ $(1); (2)\Rightarrow \widehat{BAE}=\widehat{AEB}$
$\Rightarrow \triangle ABE$ cân tại $B$
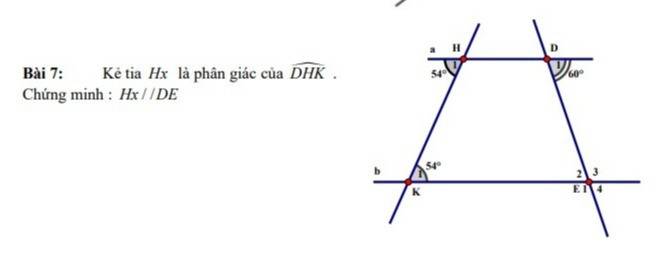
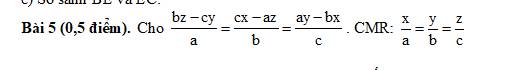
Hello My name is........in class.......from (trường của bạn) .Students join different community activities for a myriad of compelling reasons that transcend mere extracurricular involvement. Firstly, engagement in community activities fosters a sense of belonging and camaraderie among students, providing them with an opportunity to connect with peers who share similar interests or passions. This sense of community often bolsters their self-esteem and social skills, equipping them with invaluable interpersonal abilities that extend beyond the classroom. Additionally, participating in such activities enables students to cultivate a deeper understanding of societal issues and challenges, encouraging empathy and a desire for positive change. Many students also recognize the practical benefits, as community involvement can enhance their resumes, demonstrating to future employers or academic institutions their commitment, leadership qualities, and ability to collaborate effectively within diverse settings. Furthermore, community activities often offer students a platform to explore new hobbies or passions, whether it's volunteering, arts, sports, or advocacy work, allowing them to discover their strengths and interests outside of academic confines. Ultimately, by immersing themselves in various community endeavors, students not only enrich their personal development but also contribute meaningfully to the broader society, shaping them into responsible, empathetic, and well-rounded individuals.