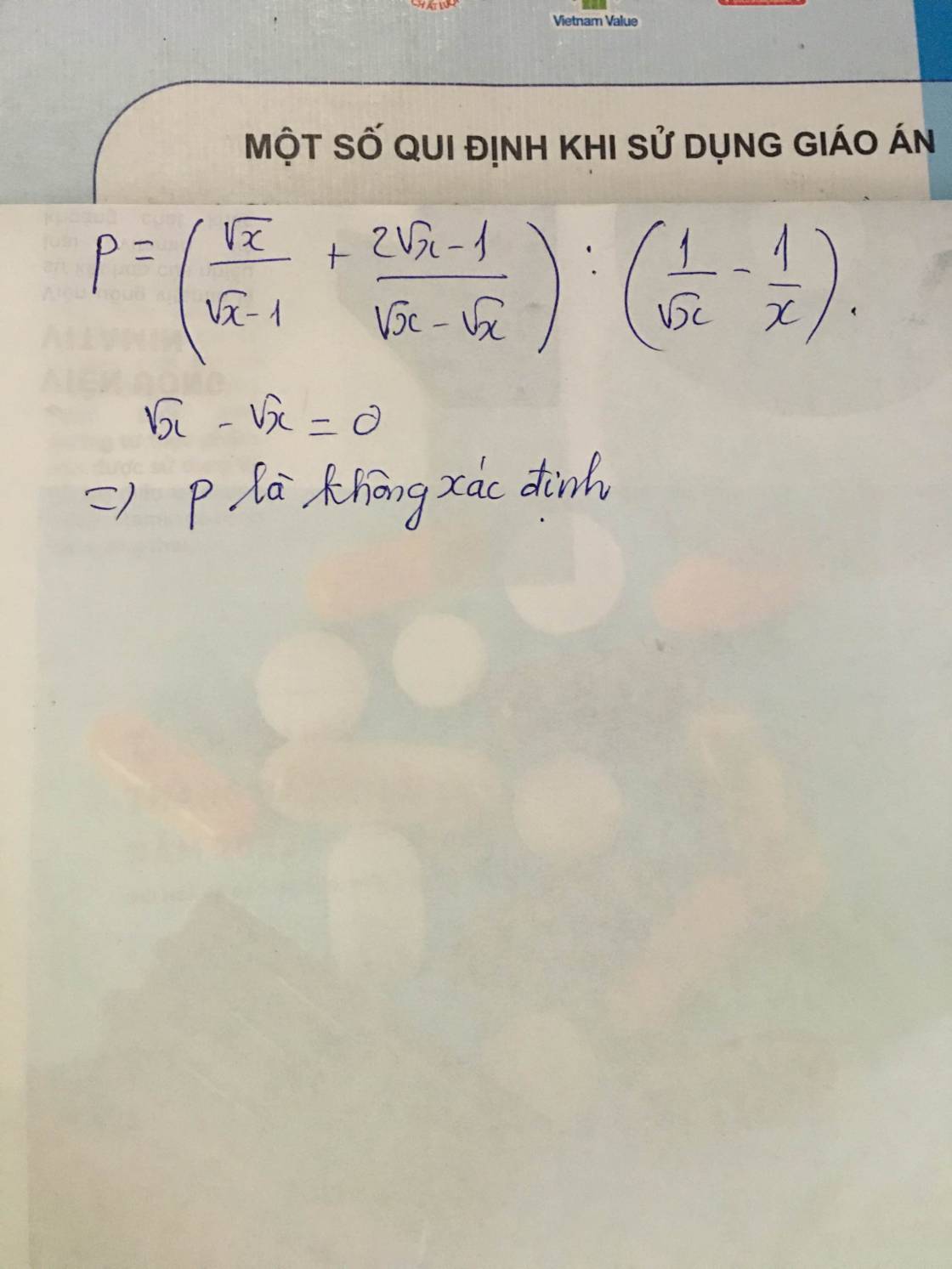Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ĐKXĐ: \(a>0;a\ne1\)
Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right):\left(\dfrac{a^2+a\sqrt{a}}{\sqrt{a}+1}\right)\)
\(=\left(\dfrac{\left(\sqrt{a}+1\right)^2-\left(\sqrt{a}-1\right)^2+4\sqrt{a}\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right).\left(\dfrac{\sqrt{a}+1}{a\sqrt{a}\left(\sqrt{a}+1\right)}\right)\)
\(=\left(\dfrac{4a\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\right).\left(\dfrac{1}{a\sqrt{a}}\right)\)
\(=\dfrac{4}{a-1}\)
Để \(P>2\) thì \(\dfrac{4}{a-1}>2\Leftrightarrow\dfrac{4}{a-1}-2>2\)
\(\Leftrightarrow\dfrac{2\left(a-3\right)}{1-a}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a-3>0\\1-a>0\end{matrix}\right.\\\left\{{}\begin{matrix}a-3< 0\\1-a< 0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a>3\\a< 1\end{matrix}\right.\\\left\{{}\begin{matrix}a< 3\\a>1\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow1< a< 3\)
Vậy khi \(1< a< 3\) thì \(P>2\)
\(R=\dfrac{3x+3\sqrt{x}-3}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\left(x>=0;x\ne1\right)\\ =\dfrac{3x+3\sqrt{x}-3-\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{3x+3\sqrt{x}-3-\left(x-1\right)-\left(x+4\sqrt{x}+4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{x-\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
\(R=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1-2}{\sqrt{x}-1}=1-\dfrac{2}{\sqrt{x}-1}\\ R\in Z=>\dfrac{2}{\sqrt{x}-1}\in Z\\ =>2⋮\left(\sqrt{x}-1\right)=>\sqrt{x}-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\\ =>\sqrt{x}\in\left\{2;3;0;-1\right\}\\ =>x\in\left\{4;9;0\right\}\left(TMDK\right)\)
\(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\left(a>0,b>0,a\ne b\right)\\ =\dfrac{\sqrt{ab}.\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\\ =\left(\sqrt{a}+\sqrt{b}\right).\left(\sqrt{a}-\sqrt{b}\right)=a-b\)
\(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right).\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(a>=0;a\ne1\right)\\ =\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right).\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\\ =\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)
Để đồ thị hai hàm số là các đường thẳng song song :
{m+1=2−m2−m≠−2{m+1=2−m2−m≠−2
⇔{m=1−m2−m+2≠0⇔{m=1−m2−m+2≠0
⇔⎧⎪⎨⎪⎩m=1(l)m≠1m≠−2⇔{m=1(l)m≠1m≠−2
Không tồn tại giá trị của m để hai hàm số..........
b/ Hai đường thẳng trên cắt nhau tại 1 điểm trên trục tung khi
\(\left(m+2\right)x+2m^2+1=3x+3\) với x=0 và \(m+2\ne3\Rightarrow m\ne1\)
\(\Rightarrow2m^2=2\Rightarrow m^2=1\Rightarrow m=-1\)
ĐKXĐ: \(a>0;a\ne4\)
Ta có: \(P=\left(\dfrac{\sqrt{a}+a}{1+\sqrt{a}}\right)\left(\dfrac{a-3\sqrt{a}+2}{\sqrt{a}-2}\right)\)
\(=\left(\dfrac{\sqrt{a}\left(1+\sqrt{a}\right)}{1+\sqrt{a}}\right)\left(\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{\sqrt{a}-2}\right)\)
\(=\sqrt{a}.\left(\sqrt{a}-1\right)\)
Vậy \(P=\sqrt{a}\left(\sqrt{a}-1\right)\)
+) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\) ( đk : a > 0 ; b >0 ; a khác b )
\(=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\)
\(=a-b\)
+) \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right).\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\) ( đk : a \(\ge\)0 ; a khác 1 )
\(=\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right).\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=1-a\)
