Hi

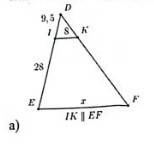
a, Vì IK // EF

  ⇒ \(\dfrac{DI}{DE}\) = \(\dfrac{IK}{EF}\) (theo định lí talet)

  ⇒ \(\dfrac{DI}{DI+IE}\) = \(\dfrac{IK}{EF}\)

⇒ \(\dfrac{9,5}{9,5+28}\) = \(\dfrac{8}{x}\)

⇒ \(\dfrac{9,5}{37,5}\) = \(\dfrac{8}{x}\)

⇒ \(x\) = 8 : \(\dfrac{9,5}{37,5}\)

    \(x\) = 31,57 

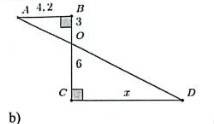
Vì AB \(\perp\) BC;

   CD \(\perp\) BC

⇒ AB // CD (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)

⇒ \(\dfrac{AB}{CD}\) = \(\dfrac{BO}{OC}\)

   \(\dfrac{4,2}{x}\)  = \(\dfrac{3}{6}\)

   \(\dfrac{4,2}{x}\) =  \(\dfrac{1}{2}\)

     \(x\)    = 4,2 x 2 : 1 

      \(x\)   = 8,4

42 x 37 = 1554,0

34 x 84 = 2856,0

         Tỉ số số bánh và số kẹo là:

                   \(\dfrac{4}{5}\) : \(\dfrac{2}{3}\) = \(\dfrac{6}{5}\)

         Ta có sơ đồ:

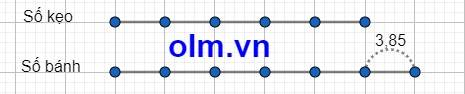
         Theo sơ đồ ta có: 

           Số kẹo là:

                3,85 : (6 - 5) x 5 = 19,25 (kg)

          Số bánh là: 19,25 + 3,85 = 23,1 (kg)

                Đáp số:...

2/

Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)

\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)

Ta có bảng:

Vậy \(n\in\left\{-1;1;2;4\right\}\)

1/

(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500

<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500

Xét tổng A = 1 + 3 + 5 + ... + 999

Số số hạng của A là: (999 - 1) : 2 + 1 = 500 

Tổng A là: (999 + 1) x 500 : 2 = 250 000

Do A có 500 số hạng nên có 500 ẩn x.

Vậy ta có: 500x + 250 000 = 500

=> 500x = -249 500

=> x = 499

Vậy x = 499

a) Xét 2 tam giác ABE và ACF, ta có:

\(\widehat{AEB}=\widehat{ACF}=90^o\) và \(\widehat{A}\) chung 

nên \(\Delta ABE~\Delta ACF\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\) \(\Rightarrow AB.AF=AC.AE\) (đpcm)

b) Từ \(AB.AF=AC.AE\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\). Từ đó dễ dàng chứng minh \(\Delta AEF~\Delta ABC\left(c.g.c\right)\)

c) Kẻ đường kính AP của (O). Ta có \(\left\{{}\begin{matrix}AB\perp BP\\AB\perp HC\end{matrix}\right.\) \(\Rightarrow\) BP//HC

 CMTT, ta có CP//HB, dẫn đến tứ giác BHCP là hình bình hành. Lại có A' là trung điểm BC \(\Rightarrow\) A' cũng là trung điểm HP.

 Do đó OA' là đường trung bình của tam giác PAH \(\Rightarrow AH=2A'O\left(đpcm\right)\)

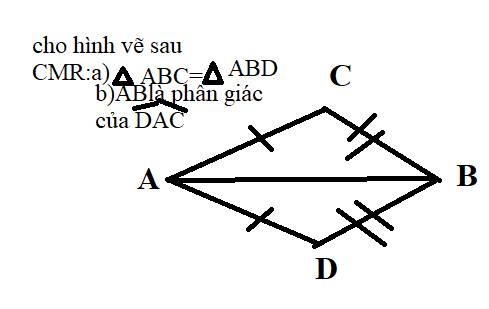
a) Xét ∆ABC và ∆ABD có:

AB là cạnh chung

AC = AD (gt)

BC = BD (gt)

⇒ ∆ABC = ∆ABD (c-c-c)

b) Do ∆ABC = ∆ABD (cmt)

⇒ ∠BAC = ∠BAD (hai góc tương ứng)

⇒ AB là tia phân giác của ∠DAC

Sau khi Thảo cho An thì An có số quả là: 5 + 2 = 7(quả)

Sau khi ăn, An còn lại số quả cam là: 7 - 1 = 6(quả)

đ/s: 6 quả

6