Gọi x (m) là độ dài cạnh hình vuông lớn nhất có thể chia (x ∈ ℕ*)

⇒ x = ƯCLN(150; 90)

Ta có:

150 = 2.3.5²

90 = 2.3².5

⇒ x = ƯCLN(150; 90) = 2.3.5 = 30

Vậy độ dài cạnh lớn nhất có thể chia là 30 m

Gọi x (m) là độ dài cạnh hình vuông lớn nhất có thể chia (x ∈ ℕ*)

⇒ x = ƯCLN(150; 90)

Ta có:

150 = 2.3.5²

90 = 2.3².5

⇒ x = ƯCLN(150; 90) = 2.3.5 = 30

Vậy độ dài cạnh lớn nhất có thể chia là 30 m

37,9615

37, 9615 (k chia hết lấy 4 chữ số phần thập phân)

n + 5 = n + 3 + 2

Để (n + 5) ⋮ (n + 3) thì 2 ⋮ (n + 3)

⇒ n + 3 ∈ Ư(2) = {-2; -1; 1; 2}

⇒ n ∈ {-5; -4; -2; -1}

Lời giải:
Với $x,y$ là số tự nhiên thì:

$15x=5.3x\vdots 5; 20y=5.4y\vdots 5$

$\Rightarrow 15x+20y\vdots 5$

Mà $2021^{2022}\not\vdots 5$

$\Rightarrow$ không tồn tại $x,y$ tự nhiên thỏa mãn đề bài.

** Sửa đề: sao cho $p+2, p+10$ cũng là snt.

Lời giải:

Nếu $p$ chia hết cho $3$ thì do $p$ là snt nên $p=3$. Khi đó: $p+2=5; p+10=13$ cũng là snt (thỏa mãn) 

Nếu $p$ chia $3$ dư $1$. Đặt $p=3k+1$ với $k$ tự nhiên.

Khi đó: $p+2=3k+3=3(k+1)\vdots 3$. Mà $p+2>3$ với mọi $p$ nguyên tố.

$\Rightarrow p+2$ không là snt theo yêu cầu đề (loại) 

Nếu $p$ chia $3$ dư $2$. Đătk $p=3k+2$ với $k$ tự nhiên.

Khi đó: $p+10=3k+2+10=3k+12=3(k+4)\vdots 3$. Mà $p+10>3$ nên $p+10$ không là snt theo yêu cầu đề (loại) 
Vậy $p=3$ là đáp án duy nhất.

nui

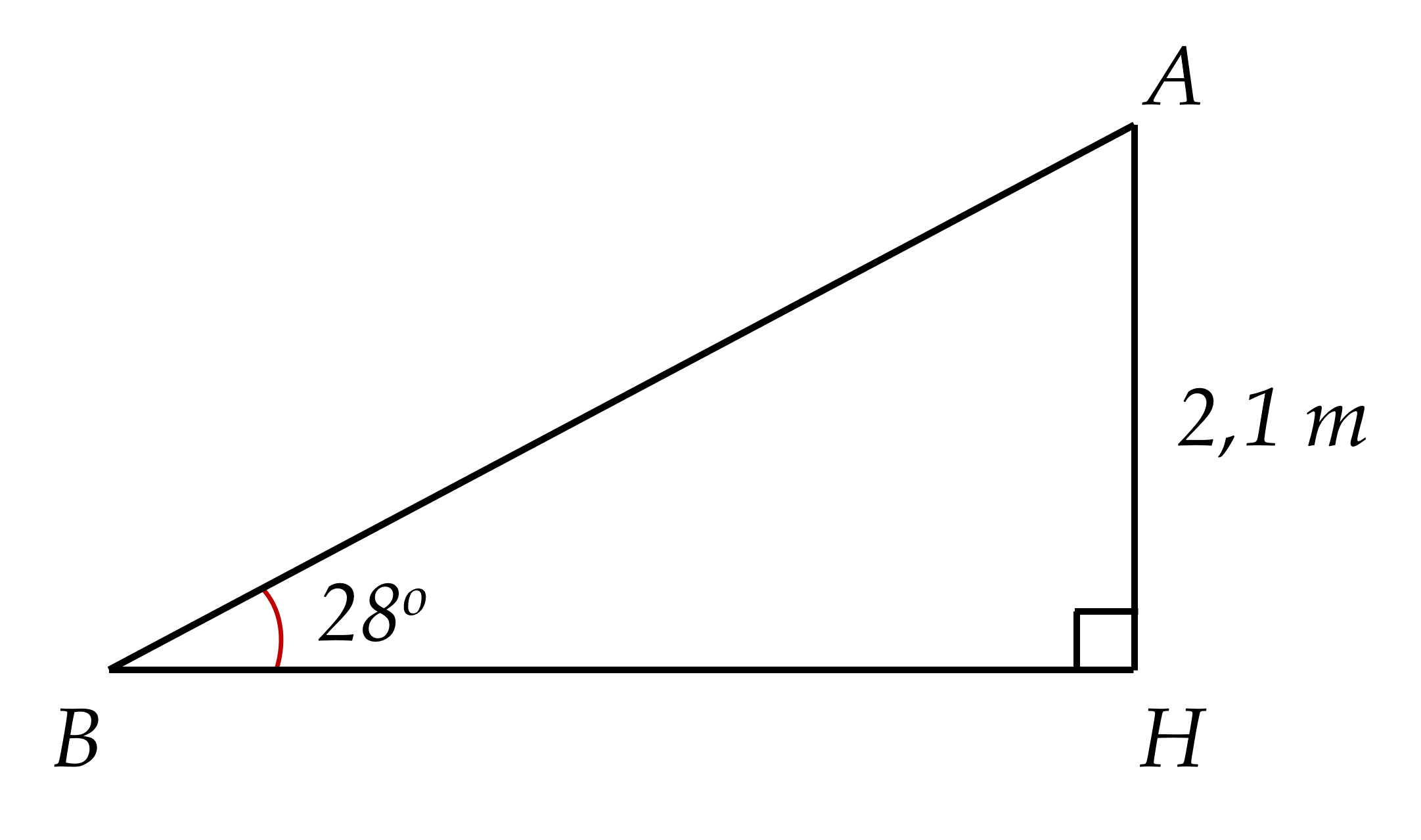
1) Xét △ABH vuông tại H có:

      \(\sin\widehat{ABH}=\dfrac{AH}{AB}\)(tỉ số lượng giác)

 ⇒ \(AB=\dfrac{AH}{\sin\widehat{ABH}}=\dfrac{2,1}{\sin28^o}\approx4,5\left(m\right)\)

Vậy độ dài của mặt cầu trượt khoảng 4,5m.

2) 

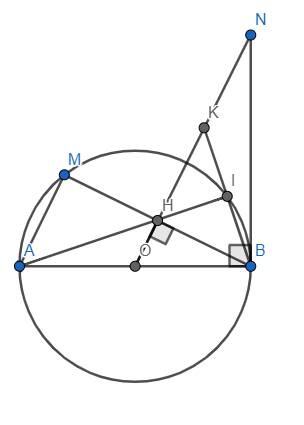
a) Xét △AMB có: A, M, B ∈ (O) (gt)

                              AB là đường kính của (O) (gt)

  ⇒ △AMB vuông tại M(ĐL về sự xác định của đường tròn)

   Xét △AMB vuông tại M có: O là trung điểm AB(gt)

                                                  OH // AM (⊥ MB)

  ⇒ OH là đường trung bình của △AMB

  ⇒ H là trung điểm của MB (t/c)(đpcm)

  Xét △NMB có: H là trung điểm của MB(cmt)

                         NH ⊥ MB(do N ∈ OH ⊥ MB)

  ⇒ NH là đường trung tuyến đồng thời cũng là đường cao trong △NMB

  ⇒ △NMB cân tại N(t/c △ cân)

  ⇒ NM = NB(t/c △ cân)

  Xét △NMO và △NBO có:

      ON chung

      NM = NB(cmt)

      OM = OB(= R)

  ⇒ △NMO = △NBO (c.c.c)

  ⇒ \(\widehat{NMO}=\widehat{NBO}=90^o\)

  ⇒ NM ⊥ MO

  Mà OM = R

  ⇒ MN là tiếp tuyến của đường tròn (O; R) (đpcm)

b) Xét △MAB và △HBN có: 

     \(\widehat{AMB}=\widehat{BHN}=90^o\)

     \(\widehat{MBA}=\widehat{HNB}\) (do cùng phụ với \(\widehat{NOB}\))

 ⇒ △MAB ∼ △HBN (g.g)(đpcm)

Bài 2:

1) Thay m = 1(TMĐK) vào hàm số y = (m - 2)x + m + 3 có

                                                     ⇒ y = (1 - 2)x + 1 + 3

                                                     ⇒ y = -x + 4

Xét (d) : y = -x + 4 có bảng 

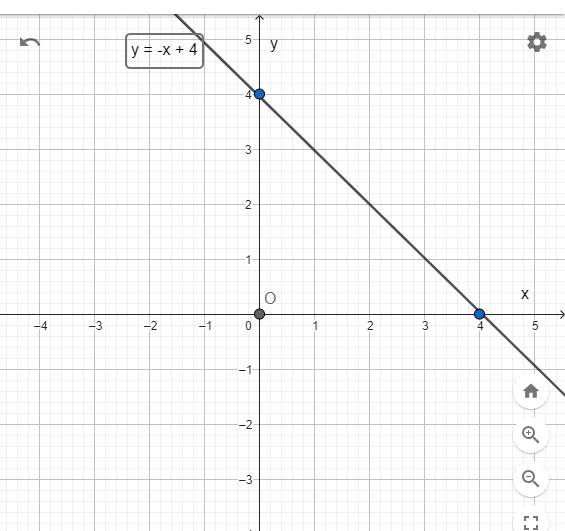
2) Để hai đường thẳng ${\mathrm{(d)}}^{}:y=\mathrm{(m\; -\; 2)}x+\mathrm{m\; +\; 3}$ và ${\mathrm{(d\text{'})}}^{}:y={\mathrm{5x}}^{}-\; 1$ cắt nhau tại một điểm trên trục tung thì

 ⇒\(\left\{{}\begin{matrix}m-2\ne5\\m+3=-1\end{matrix}\right.\)

 ⇒\(\left\{{}\begin{matrix}m\ne7\\m=-2\end{matrix}\right.\)(TM) ⇒ m = -2

Vậy m = -2 thì hai đường thẳng (d)
$:y=\mathrm{(m\; -\; 2)}x+\mathrm{m\; +\; 3}$ và ${\mathrm{(d\text{'})}}^{}:y={\mathrm{5x}}^{}-\; 1$ cắt nhau tại một điểm trên trục tung.

Bài 2:

1) Thay m = 1(TMĐK) vào hàm số y = (m - 2)x + m + 3 có

                                                     ⇒ y = (1 - 2)x + 1 + 3

                                                     ⇒ y = -x + 4

Xét (d) : y = -x + 4 có bảng 

2) Để hai đường thẳng ${\mathrm{(d)}}^{}:y=\mathrm{(m\; -\; 2)}x+\mathrm{m\; +\; 3}$ và ${\mathrm{(d\text{'})}}^{}:y={\mathrm{5x}}^{}-\; 1$ cắt nhau tại một điểm trên trục tung thì

 ⇒\(\left\{{}\begin{matrix}m-2\ne5\\m+3=-1\end{matrix}\right.\)

 ⇒\(\left\{{}\begin{matrix}m\ne7\\m=-2\end{matrix}\right.\)(TM) ⇒ m = -2

Vậy m = -2 thì hai đường thẳng (d)
$:y=\mathrm{(m\; -\; 2)}x+\mathrm{m\; +\; 3}$ và ${\mathrm{(d\text{'})}}^{}:y={\mathrm{5x}}^{}-\; 1$ cắt nhau tại một điểm trên trục tung.

48:7=4