Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






a) Xét hàm \(f\left(x\right)=\dfrac{x^{2021}-x+16}{x^{2020}-x+7}\)
\(f\left(x\right)-4=\dfrac{x^{2021}-x+16-4x^{2020}+4x-28}{x^{2020}-x+7}\)
\(=\dfrac{x^{2021}-4x^{2020}+3x-12}{x^{2020}-x+7}\)
\(=\dfrac{\left(x^{2020}+3\right)\left(x-4\right)}{\left(x^{2020}+3\right)-\left(x-4\right)}\)
Vậy nếu \(x>4\) thì \(f\left(x\right)-4>0\Leftrightarrow f\left(x\right)>4\).
Ta có \(u_1>4\) \(\Rightarrow u_2=f\left(u_1\right)>4\) \(\Rightarrow u_3=f\left(u_2\right)>4\) và cứ như thế, ta thu được \(u_n>4,\forall n\)
Mặt khác, xét hiệu \(f\left(x\right)-x\), ta có \(f\left(x\right)-x\)
\(=\dfrac{x^{2021}-x+16}{x^{2020}-x+7}-x\)
\(=\dfrac{x^{2021}-x+16-x^{2021}+x^2-7x}{x^{2020}-x+7}\)
\(=\dfrac{x^2-8x+16}{x^{2020}-x+7}\)
\(=\dfrac{\left(x-4\right)^2}{x^{2020}-x+7}>0\)
\(\Rightarrow f\left(x\right)>x\)
\(\Rightarrow u_{n+1}=f\left(u_n\right)>u_n,\forall n\)
\(\Rightarrow\left(u_n\right)\) là dãy tăng.
Giả sử \(\left(u_n\right)\) bị chặn trên. Khi đó đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L>2021\). Khi đó:
\(L=\dfrac{L^{2021}-L+16}{L^{2020}-L+7}\)
\(\Leftrightarrow L^{2021}-L^2+7L=L^{2021}-L+16\)
\(\Leftrightarrow L^2-8L+16=0\)
\(\Leftrightarrow L=4\), vô lý.
Vậy \(\left(u_n\right)\) không bị chặn trên \(\Rightarrow\lim\limits_{n\rightarrow+\infty}u_n=+\infty\) hay \(\left(u_n\right)\) không có ghhh.
b) Ta có \(\dfrac{1}{f\left(x\right)-4}=\dfrac{\left(x^{2020}+3\right)-\left(x-4\right)}{\left(x^{2020}+3\right)\left(x-4\right)}\)
\(=\dfrac{1}{x-4}-\dfrac{1}{x^{2020}+3}\)
Từ đó ta có \(\dfrac{1}{u_{n+1}-4}=\dfrac{1}{u_n-4}-\dfrac{1}{u_n^{2020}+3}\)
\(\Leftrightarrow\dfrac{1}{u_n^{2020}+3}=\dfrac{1}{u_n-4}-\dfrac{1}{u_{n+1}-4}\)
\(\Rightarrow S_n=\sum\limits^n_{i=1}\dfrac{1}{u_i^{2020}+3}=\dfrac{1}{u_1-4}-\dfrac{1}{u_{n+1}-4}\)
\(=\dfrac{1}{2017}-\dfrac{1}{u_{n+1}-4}\)
\(\Rightarrow\lim\limits_{n\rightarrow+\infty}S_n=\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{2017}-\dfrac{1}{u_{n+1}-4}\right)=\dfrac{1}{2017}\)
(vì \(\lim\limits_{n\rightarrow+\infty}u_n=+\infty\))
Vậy \(\lim\limits_{n\rightarrow+\infty}S_n=\dfrac{1}{2017}\)

S A B C D E F G H M N P Q
Xét tg SNP có
\(\dfrac{SG}{GP}=\dfrac{SF}{FN}=2\) => GF//NP (Talet đảo trong tg)
Mà \(NP\in\left(ABCD\right)\) => GF//(ABCD)
C/m tương tự ta cũng có
EF//(ABCD); GH//(ABCD); HE//(ABCD)

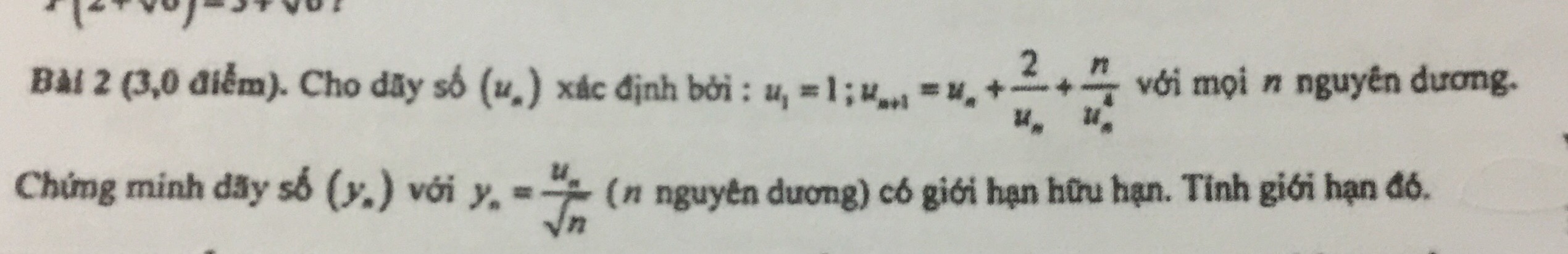
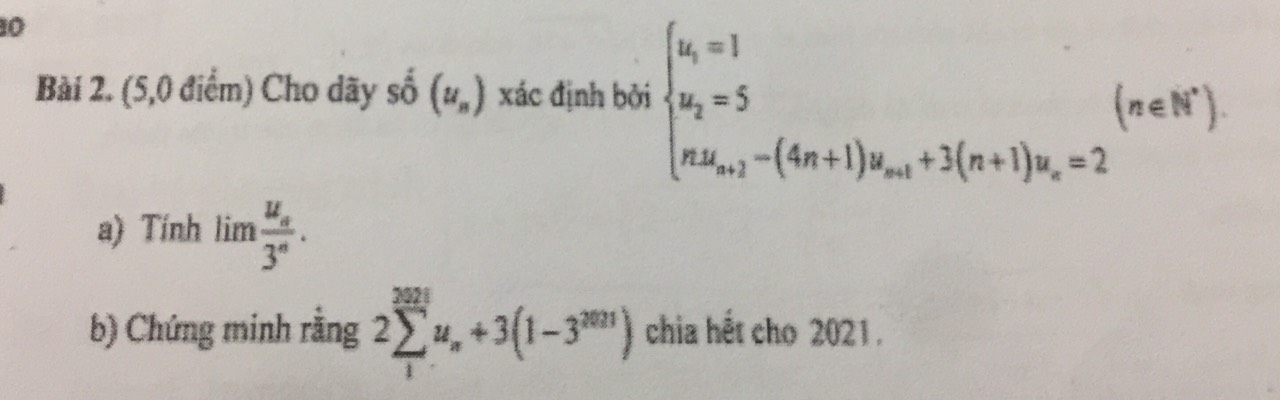
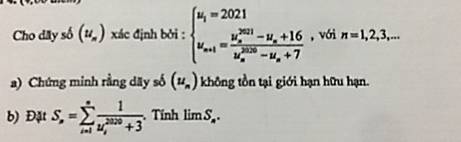
Ta có \(s_n\) hội tụ nên \(\lim\limits_{n\rightarrow+\infty}x_n=+\infty\)
Nếu \(2-\cos2\alpha\ne0\) thì
\(\lim\limits_{n\rightarrow+\infty}x_{n+1}=\lim\limits_{n\rightarrow+\infty}\dfrac{\left(2+\cos2\alpha\right)x_n+\cos^2\alpha}{\left(2-2\cos\alpha\right)x_n+2-\cos2\alpha}=\dfrac{2+\cos\alpha}{2-2\cos2\alpha}\), vô lí.
Do đó \(2-2\cos2\alpha=0\) \(\Leftrightarrow\alpha=k\pi\left(k\inℤ\right)\)
Với \(\alpha=k\pi\left(k\inℤ\right)\)
Ta có \(x_{n+1}=3x_n+1\) \(\Leftrightarrow2x_{n+1}+1=3\left(2x_n+1\right)=...=3^{n+1}\left(2x_1+1\right)=3^{n+1}\). Do đó:
\(s_n=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}=\dfrac{1-\dfrac{1}{3^n}}{2}\)
Vậy nên \(\left(s_n\right)\) có giới hạn hữu hạn và \(\lim\limits_{n\rightarrow+\infty}=\dfrac{1}{2}\)