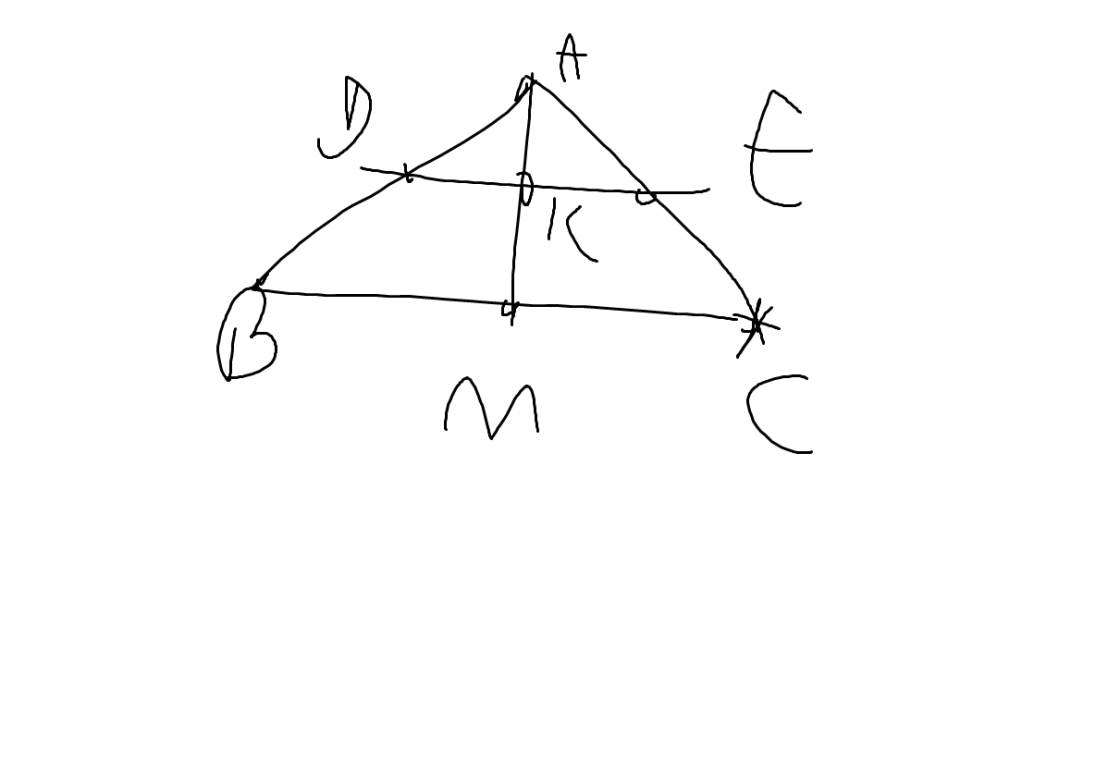
Cho tam giác ABC cân tại A,AM trung tuyến với M ϵ BC.Trên AB lấy điểm D,trên AC lấy điểm E sao cho AD=AE
a,CM:Δ AMB =ΔAMC
b,CM:AM là phân giác của ABC và AM ⊥ BC
c,Gọi K là giao điểm của AM và DE.CM AK⊥ DE(vẽ hình cho mik với ạ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để \(\dfrac{-5n+27}{n+3}\in Z\) thì \(-5n+27⋮n+3\)
=>\(-5n-15+42⋮n+3\)
=>\(42⋮n+3\)
=>\(n+3\in\left\{1;-1;2;-2;3;-3;6;-6;7;-7;14;-14;21;-21;42;-42\right\}\)
=>\(n\in\left\{-2;-4;-1;-5;0;-6;3;-9;4;-10;11;-17;18;-24;39;-45\right\}\)

Gọi độ dài của 3 loại vải lần lượt là: \(x,y,z\) \(\left(x,y,z>0\right)\)
Diện tích của 3 loại vải mà người đó mua lần lượt là: \(0,7x;0,8y;1,4z\)
Diện tích của 3 loại vải đã mua là bằng nhau ta có:
\(0,7x=0,8y=1,4z\)
\(\Rightarrow\dfrac{7}{10}x=\dfrac{4}{5}y=\dfrac{7}{5}z\)
\(\Rightarrow\dfrac{x}{\dfrac{10}{7}}=\dfrac{y}{\dfrac{5}{4}}=\dfrac{z}{\dfrac{5}{7}}\)
Tổng độ dài của số vải là 5,7 m ta có: \(x+y+z=5,7\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{10}{7}}=\dfrac{y}{\dfrac{5}{4}}=\dfrac{z}{\dfrac{5}{7}}=\dfrac{x+y+z}{\dfrac{10}{7}+\dfrac{5}{4}+\dfrac{5}{7}}=\dfrac{5,7}{\dfrac{95}{28}}=1,68\)
\(\Rightarrow\dfrac{x}{\dfrac{10}{7}}=1,68\Rightarrow x=1,68\cdot\dfrac{10}{7}=2,4\left(m\right)\)
\(\Rightarrow\dfrac{y}{\dfrac{5}{4}}=1,68\Rightarrow y=1,68\cdot\dfrac{5}{4}=2,1\left(m\right)\)
\(\Rightarrow\dfrac{z}{\dfrac{5}{7}}=1,68\Rightarrow z=1,68\cdot\dfrac{5}{7}=1,2\left(m\right)\)
Vậy: ...

Gọi k là hệ số tỉ lệ
x và y là hai đại lượng tỉ lệ nghịch ta có:
`xy=k`
`=>k=(-12)*10=-120`
Gọi k là hệ số tỉ lệ của x và y
Do x và y là hai đại lượng tỉ lệ nghịch nên:
k = x.y = 10.(-12) = -120

A = |\(x\) - 2021| + |\(x\) - 2022| + |\(x\) - 2023|
A = |\(x\) - 2021| + |2023 - \(x\)| + |\(x-2022\)|
Đặt B = |\(x-2021\)| + |2023 - \(x\)|
B ≥ |\(x-2021\) + 2023 - \(x\)| = |2| = 2 dấu bằng xảy ra khi
2021 ≤ \(x\) ≤ 2023
A = B + |\(x\) - 2022|
A ≥ |2| + 0 = 2
Dấu bằng xảy ra khi \(x\) - 2022 = 0; \(x\) = 2022 (thỏa mãn)
Vậy Amin = 2 khi \(x=2022\)


Đề sai. Cho $x=1,y=-1, z=0$ thì điều kiện đề cho vẫn đúng nhưng $x\neq y\neq z$
a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
=>AM là phân giác của góc BAC
c: Xét ΔADE có AD=AE
nên ΔADE cân tại A
Ta có: ΔADE cân tại A
mà AK là đường phân giác
nên AK\(\perp\)DE