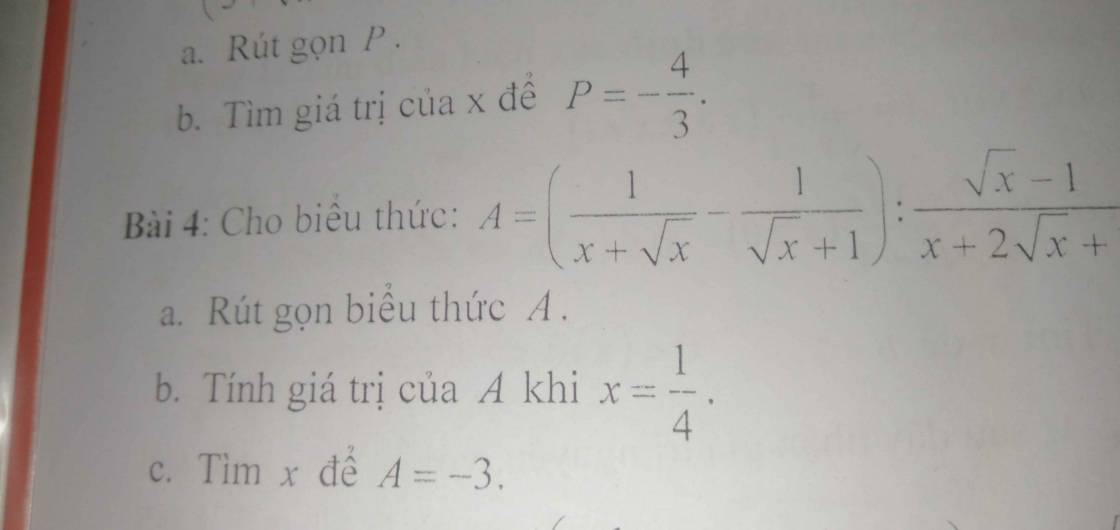Cho $x, y$ là các số dương và $(\sqrt{x}+1)(\sqrt{y}+1) \geq 4$.
Tìm giá trị nhỏ nhất của biểu thức $M=\dfrac{x^3+y^3}{x y}$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
24 tháng 10 2022
Ta có:
\(\dfrac{1}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\\ =\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(\dfrac{\sqrt{x}-1}{x+2\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)^2}\)
Vậy \(A=\left(\dfrac{1}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}-1}{x+2\sqrt{x}+1}\\ =\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)^2}\\ =\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\\ =\dfrac{-(\sqrt{x}-1)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\\ =\dfrac{-\left(\sqrt{x}+1\right)}{\sqrt{x}}=-1-\dfrac{1}{\sqrt{x}}\)
b.
\(x=\dfrac{1}{4}\) \(\Rightarrow A=-1-\dfrac{1}{\sqrt{\dfrac{1}{4}}}=-1-\dfrac{1}{\dfrac{1}{2}}=-3\)
c. Từ câu b ta có A= -3 khi x = 1/4
NM
0
LD
0
