Sau 24 ngày cả hai cùng nhau đến thư viện.

24 ngày

\(\sqrt{0,36}+5\sqrt{1,21}=0,6+5.1,1=0,65,5=6,1\)

a) 2 + (81 - x) = -34

81 - x = -34 - 2

81 - x = -36

x = 81 - (-36)

x = 81 + 36

x = 117

b) (-12).x = 60

x = 60 : (-12)

x = -5

c) 12 : (x - 1)² = 3

(x - 1)² = 12 : 3

(x - 1)² = 4

(x - 1)² = 2² (cùng số mũ)

⇒ x - 1 = 2

x = 2 + 1

x = 3

2+(81-x)=-34

      81-x=(-34)-2

      81-x=-36

            x=81-(-36)

            x= 117

                  Ta có:218 : 3,7=58,91(dư 0,33)

Vậy dư của phép tính 218 : 3,7 là 0,33

                                         Đáp số:...

\(\sqrt{\dfrac{25}{4}}-\sqrt{\dfrac{49}{16}}=\dfrac{5}{2}-\dfrac{7}{4}=\dfrac{10}{4}-\dfrac{7}{4}=\dfrac{3}{4}\)

căn 25/4-căn 49/16=căn(5/2)mũ 2-căn(7/4)mũ 2=5/2-7/4=3/4

21,71806167

Ngày thứ nhất đội đó gặt được số ha lúa là:

2,5 x 40 : 100 = 1 (ha)

Ngày thứ hai đội đó gặt được số ha lúa là:

 2,5 - 1 = 1,5 (ha)

Đs..

Sau 40 ngày 2 bạn sẽ đến thư viện.

dựa vào đâu 

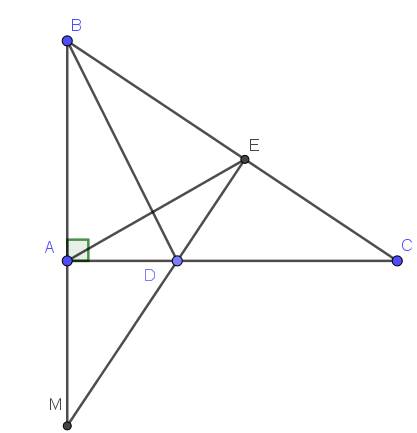
Lời giải:
a. Xét tam giác $ABD$ và $EBD$ có:

$AB=EB$ 

$BD$ chung

$\widehat{ABD}=\widehat{EBD}$ (do $BD$ là phân giác $\widehat{B}$)

$\Rightarrow \triangle ABD=\triangle EBD$ (c.g.c)

b.

Từ tam giác bằng nhau phần a suy ra:

$AD=DE$

$\widehat{BED}=\widehat{BAD}=90^0$

$\Rightarrow DE\perp BC$

$\Rightarrow \widehat{DEC}=90^0$
Xét tam giác $ADM$ và $EDC$ có:

$AD=ED$ (cmt)

$\widehat{ADM}=\widehat{EDC}$ (đối đỉnh)

$\widehat{DAM}=\widehat{DEC}=90^0$

$\Rightarrow \triangle ADM=\triangle EDC$ (g.c.g)

$\Rightarrow AM=EC$

c.

Từ tam giác bằng nhau phần b suy ra:

$\widehat{M_1}=\widehat{C_1}$

$DM=DC$

Mà $DE=AD$

$\Rightarrow DM+DE=DC+AD$

$\Rightarrow ME=AC$

Xét tam giác $AEM$ và $EAC$ có:

$AM=EC$ (cmt)

$EM=AC$ (cmt)

$\widehat{M_1}=\widehat{C_1}$ (cmt)

$\Rightarrow \triangle AEM=\triangle EAC$ (c.g.c)

$\Rightarrow \widehat{EAM}=\widehat{AEC}$

Hình vẽ:

7\(x\) - 2y = 15

y =( 7\(x\) - 15) : 2

⇒ 7\(x\) - 15 ⋮ 2

⇒ \(x\) - 1 ⋮ 2 

⇒ \(x\) = 2k + 1; k \(\in\) N

    Vì y là số tự nhiên nên 7\(x\) - 15 ≥ 0 ⇒ \(x\) ≥ \(\dfrac{15}{7}\) 

  ⇒ 2k + 1 ≥ \(\dfrac{15}{7}\)

       k ≥ (\(\dfrac{15}{7}\) - 1 ) : 2

     k ≥ \(\dfrac{8}{14}\) ⇒ k ≥ 1;

⇒ \(x\) = 2k + 1; k ϵ N*

y = \(\dfrac{7.\left(2k+1\right)-15}{2}\)

y = 7k - 4

Vậy câc cặp số tự nhiên \(x;y\) thỏa mãn đề bài là

(\(x;y\)) = (2k+1; 7k - 4); k \(\in\)N*