Do ƯCLN(a,b) = 12

=> a = 12 × a'; b = 12 × b' (a';b')=1

Ta có:

a + b = 120

12 × a' + 12 × b' = 120

12 × (a' + b') = 120

a' + b' = 120 : 12

a' + b' = 10

Giả sử a > b => a' > b' mà (a';b')=1 => a' = 9; b' = 1 hoặc a' = 7; b' = 3

+ Với a' = 9; b' = 1 => a = 108; b = 12

+ Với a' = 7; b' = 3 => a = 84; b = 36

Vậy các cặp giá trị a,b thỏa mãn là: (108;12) ; (84;36) ; (36;84) ; (12;108)

ƯCLN(a,b)=34=>a chia hết cho 34;b chia hết cho 34

ta có a=m.34;b=n.34(m,n là số tư nhiên)

=>a.b=34.m.34.n=6936 

            m.n.1156 =6936

            m.n          =6936:1156

            m.n           =6=1.6=6.1=2.3=3.2

vậy:(m,n):(1;6),(6;1),(2;3),(3;2)

do 72= 3${}^{{}^2}$.2${}^3$

nếu ít nhất trong 2 số a , b có 1 số chia hết cho 2 

giả sử a chia hết cho 2 =>b=42-a cũng chia hết cho 2

=> cả a và b đều chia hết cho 2

vì vậy tương tự ta cũng có a,b chi hết cho 3

=>a và b chia hết cho 6

ta thấy 42=36+6=30+12=18+24(là tổng 2 số chia hết cho 6)

trong các số trên chỉ có số 18 và 24 thỏa mãn

=>a=18;b=24

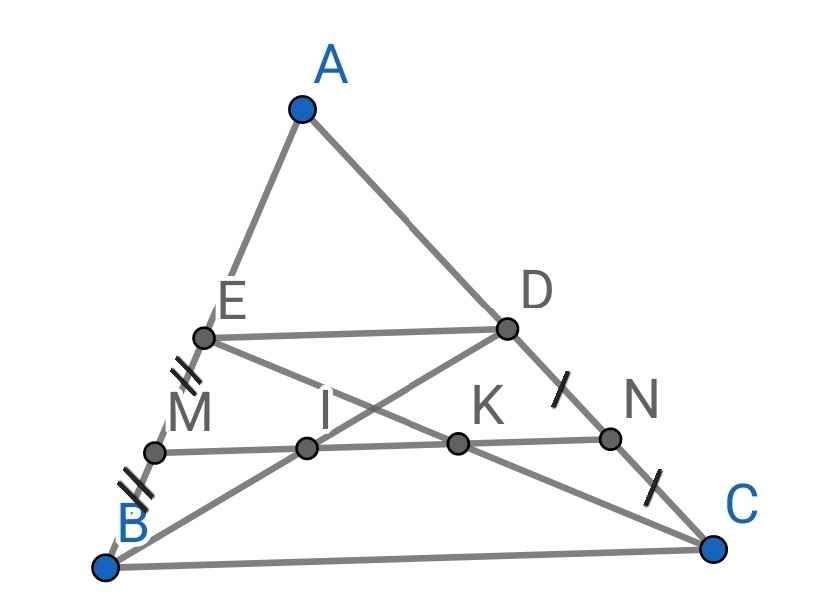
Do BD là đường trung tuyến của ∆ABC (gt)

⇒ D là trung điểm của AC

Do CE là đường trung tuyến của ∆ABC (gt)

⇒ E là trung điểm của AB

⇒ DE là đường trung bình của ∆ABC

⇒ DE // BC và DE = BC : 2

⇒ BC = 2DE

Do DE // BC (cmt)

⇒ BCDE là hình thang

Do M là trung điểm của BE (gt)

N là trung điểm của CD (gt)

⇒ MN là đường trung bình của hình thang BCDE

⇒ MN // DE // BC và MN = (DE + BC) : 2

Do MN // DE (cmt)

⇒ MI // DE và NK // DE

∆BDE có:

MI // DE (cmt)

M là trung điểm của BE (gt)

⇒ I là trung điểm của BD

⇒ MI là đường trung bình của ∆BDE

⇒ MI = DE : 2   (1)

∆CDE có:

NK // DE (cmt)

N là trung điểm của CD (gt)

⇒ K là trung điểm của CE

⇒ NK là đường trung bình của ∆CDE

⇒ NK = DE : 2   (2)

Mà MI = DE : 2

⇒ MI = NK = DE : 2

⇒ MI + NK = DE

Ta có:

MN = (DE + BC) : 2

Mà BC = 2DE (cmt)

⇒ MN = (DE + 2DE) : 2

= DE + DE : 2

Lại có:

MN = MI + IK + NK

= (MI + NK) + IK

= DE + IK

⇒ DE + IK = DE + DE : 2

⇒ IK = DE : 2 (3)

Từ (1), (2) và (3) ⇒ MI = IK = KN

Xét $\Delta BED$ có {��//����=��{​MI//EDME=BM​ suy ra $ID=IB$.

Xét $\Delta CED$ có {��//����=��{​NK//EDNC=ND​ suy ra $KE=KC$.

Suy ra $MI=\genfrac{}{}{0ex}{}{1}{2}ED$; $NK=\genfrac{}{}{0ex}{}{1}{2}ED$; $ED=\genfrac{}{}{0ex}{}{1}{2}BC$.

$IK=MK-MI=\genfrac{}{}{0ex}{}{1}{2}BC-\genfrac{}{}{0ex}{}{1}{2}DE=DE-\genfrac{}{}{0ex}{}{1}{2}DE=\genfrac{}{}{0ex}{}{1}{2}DE$.

Vậy $MI=IK=KN$.

2x - 9 = 3² : 3

2x - 9 = 9 : 3

2x - 9 = 3

2x = 3 + 9

2x = 12

x = 12 : 2

x = 6 

a) Số gạo bán buổi chiều:

300 - 180 = 120 (kg)

Số phần trăm giữa số gạo bán buổi chiều so với cả ngày:

120 × 100% : 300 = 40%

Chọn D

--------

b) Chiều dài hình chữ nhật là:

115,6 : 8,5 = 13,6 (m)

Chọn C

a) D

b) C

A = -1 - 2 - 3 - ... - 100

= -(1 + 2 + 3 + ... + 100)

= -100.101 : 2

= -5050

--------

B = -2 - 4 - 6 - ... - 100

= -(2 + 4 + 6 + ... + 100)

Số số hạng của B:

(100 - 2) : 2 + 1 = 50 (số)

B = -(100 + 2) . 50 : 2 = -2550

--------

C = -6 - 9 - 12 - ... - 99

= -(6 + 9 + 12 + ... + 99)

Số số hạng của C:

(99 - 6) : 3 + 1 = 32 (số)

C = -(99 + 6) . 32 : 2 = -1680

--------

D = 4 - 8 + 12 - 16 + ... + 196 - 200

Số số hạng của D:

(200 - 4) : 4 + 1 = 50 (số)

D = (4 - 8) + (12 - 16) + ... + (196 - 200)

= -4 + (-4) + ... + (-4) (25 số -4)

= -4.25

= -100

a/

Xét tg ABC có

NA=NB; MA=MC => MN là đường trung bình của tg ABC => MN//BC

Xét tg GBC có

DG=DB; EG=EC => DE là đường trung bình của tg GBC => DE//BC

=> MN//DE (cùng // BC)

b/

Xét tg ABG có

NA=NB; DG=DB => ND là đường trung bình của tg ABG => ND//AG

Xét tg ACG có

MA=MC; EG=EC => ME là đường trung bình của tg ACG => ME//AG

=> ND//ME (cùng // với AG)

a) Vì $BM$, $CN$ là các đường trung tuyến của $\Delta ABC$ nên $MA=MC$, $NA=NB$.

Do đó $MN$ là đường trung bình của $\Delta ABC$, suy ra $MN$ // $BC$. (1)

Ta có $DE$ là đường trung bình của $\Delta GBC$ nên $DE$ // $BC$.  (2)

Từ (1) và (2) suy ra $MN$ // $DE$.

b) Xét $\Delta ABG$, ta có $ND$ là đường trung bình.

Xét $\Delta ACG$, ta có $ME$ là đường trung bình.

Do đó $ND$ // $AG$, $ME$ // $AG$.

Suy ra $ND$ // $ME$.

a/ Goi E là trung điểm của MC

Từ gt \(AM=\dfrac{1}{2}MC\Rightarrow AM=ME=EC\)

Xét tg BCM có

ME=EC (cmt); DB=DC (gt) => DE là đường trung bình của tg BCM

=> DE//BM 

Xét tg ADE có

AM=ME (cmt)

BM//DE (cmt) =>OM//DE

=> OA=OD (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)

b/

Ta có DE là đường trung bình của tg BCM \(\Rightarrow DE=\dfrac{1}{2}BM\)

Xét tg ADE có

OA=OD (cmt); AM=ME (cmt) => OM là đường trung bình của tg ADE

\(\Rightarrow OM=\dfrac{1}{2}DE=\dfrac{1}{2}.\dfrac{1}{2}BM=\dfrac{1}{4}BM\)

a) Qua $D$ vẽ một đường thẳng song song với $BM$ cắt $AC$ tại $N$.

Xét $\Delta MBC$ có $DB=DC$ và $DN$ // $BM$ nên $MN=NC=\genfrac{}{}{0ex}{}{1}{2}MC$ (định lí đường trung bình của tam giác).

Mặt khác $AM=\genfrac{}{}{0ex}{}{1}{2}MC$, do đó $AM=MN=\genfrac{}{}{0ex}{}{1}{2}MC$.

Xét $\Delta AND$ có $AM=MN$ và $BM$ // $DN$ nên $OA=OD$ hay $O$ là trung điểm của $AD$.

b) Xét $\Delta AND$ có $OM$ là đường trung bình nên $OM=\genfrac{}{}{0ex}{}{1}{2}DN$. (1)

Xét $\Delta MBC$ có $DN$ là đường trung bình nên $DN=\genfrac{}{}{0ex}{}{1}{2}BM$. (2)

Từ (1) và (2) suy ra $OM=\genfrac{}{}{0ex}{}{1}{4}BM$.

Gọi K là trung điểm của CD

a: Xét ΔBDC có 

M là trung điểm của BC

K là trung điểm của CD

Do đó: MK là đường trung bình

=>MK//BD

hay ID//MK

Xét ΔAMK có 

I là trung điểm của AM

ID//MK

Do đó: D là trung điểm của AK

=>AD=DK=KC

=>AD=1/2DC

b: Xét ΔAMK có 

I là trung điểm của AM

D là trung điểm của AK

Do đó: ID là đường trung bình

=>ID=MK/2

hay MK=2ID

Ta có: MK là đường trung bình của ΔBDC

nên MK=BD/2

=>BD/2=2ID

hay BD=4ID

Đúng thầy cho em like nhé !

a) Kẻ $MN$ // $BD$, $N\in AC$.

$MN$ là đường trung bình trong $△CBD$

Suy ra $N$ là trung điểm của $CD$ (1).

$IN$ là đường trung bình trong $△AMN$

Suy ra $D$ là trung điểm của $AN$ (2).

Từ (1) và (2) suy ra $AD=\genfrac{}{}{0ex}{}{1}{2}DC$.

b) Có $ID=\genfrac{}{}{0ex}{}{1}{2}MN$; $MN=\genfrac{}{}{0ex}{}{1}{2}BD$, nên $BD=ID$.

con cac

Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ nhanh hơn nhé.

Ta có

\(BC\perp AB';B'C'\perp AB'\) => BC//B'C'

\(\Rightarrow\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\Rightarrow\dfrac{x}{x+h}=\dfrac{a}{a'}\)

\(\Rightarrow a'x=ax+ah\Rightarrow x\left(a'-a\right)=ah\Rightarrow x=\dfrac{ah}{a'-a}\left(dpcm\right)\)

Xét tam giác $ABC$ có $BC\perp A{B}^{\prime }$ và $B^{\prime }{C}^{\prime }\perp A{B}^{\prime }$ nên suy ra $BC$ // $B^{\prime }{C}^{\prime }$.

Theo hệ quả định lí Thalès, ta có: $\genfrac{}{}{0ex}{}{AB}{A{B}^{\prime }}=\genfrac{}{}{0ex}{}{BC}{B{C}^{\prime }}$

Suy ra $\genfrac{}{}{0ex}{}{x}{x+h}=\genfrac{}{}{0ex}{}{a}{a^{\prime }}$

$a^{\prime }.x=a(x+h)$

$a^{\prime }.x-ax=ah$

$x(a^{\prime }-a)=ah$

$x=\genfrac{}{}{0ex}{}{ah}{a^{\prime }-a}$.