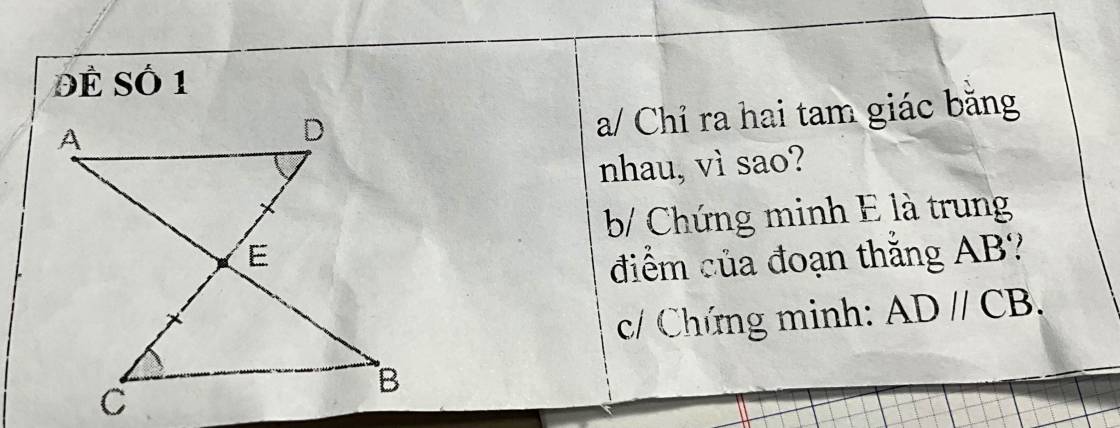
Bài 2:

a: Xét ΔOAD và ΔOCB có

OA=OB

\(\widehat{AOD}\) chung

OD=OB

Do đó: ΔOAD=ΔOCB

b: Ta có: ΔOAD=ΔOCB

=>\(\widehat{ODA}=\widehat{OBC};\widehat{OAD}=\widehat{OCB}\)

Ta có: \(\widehat{OAD}+\widehat{DAB}=180^0\)(hai góc kề bù)

\(\widehat{OCB}+\widehat{DCB}=180^0\)(hai góc kề bù)

mà \(\widehat{OAD}=\widehat{OCB}\)

nên \(\widehat{DAB}=\widehat{DCB}\)

Ta có: OA+AB=OB

OC+CD=OD

mà OA=OC và OB=OD

nên AB=CD

Xét ΔIAB và ΔICD có

\(\widehat{IAB}=\widehat{ICD}\)

AB=CD

\(\widehat{IBA}=\widehat{IDC}\)

Do đó: ΔIAB=ΔICD

c: Sửa đề: OI là phân giác của góc xOy

Ta có: ΔIAB=ΔICD

=>IB=ID và IA=IC

Xét ΔOIB và ΔOID có

OB=OD

IB=ID

OI chung

Do đó: ΔOIB=ΔOID

=>\(\widehat{BOI}=\widehat{DOI}\)

=>\(\widehat{xOI}=\widehat{yOI}\)

=>OI là phân giác của góc xOy

d: Sửa đề: OI\(\perp\)BD

ta có: OB=OD

=>O nằm trên đường trung trực của BD(1)

ta có: IB=ID

=>I nằm trên đường trung trực của BD(2)

Từ (1),(2) suy ra OI là đường trung trực của BD

=>OI\(\perp\)BD

e: Xét ΔOBD có \(\dfrac{OA}{AB}=\dfrac{OC}{CD}\)

 nên AC//BD

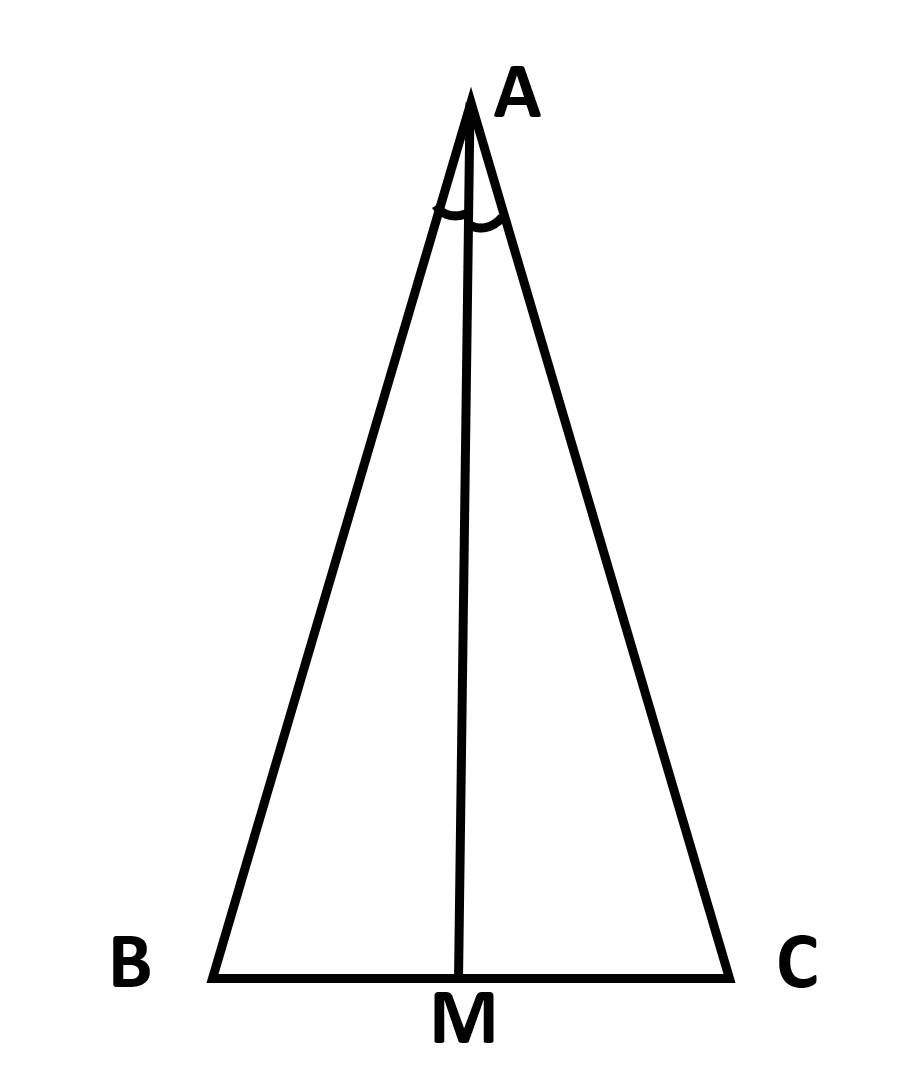
Bài 1:

a: ΔABC vuông cân tại A

=>AB=AC và \(\widehat{ABC}=\widehat{ACB}=45^0\)

Ta có: BO là phân giác của góc ABC

=>\(\widehat{ABO}=\widehat{CBO}=\dfrac{\widehat{ABC}}{2}=22,5^0\)

ta có: CO là phân giác của góc ACB

=>\(\widehat{ACO}=\widehat{BCO}=\dfrac{\widehat{ACB}}{2}=22,5^0\)

b: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\left(=22,5^0\right)\)

nên ΔOBC cân tại O

c: Ta có: ΔOBC cân tại O

=>\(\widehat{BOC}=180^0-2\cdot\widehat{OBC}=180^0-2\cdot22,5^0=135^0\)

d: Xét ΔAMC vuông tại A và ΔANB vuông tại A có

AC=AB

\(\widehat{ACM}=\widehat{ABN}\left(=22,5^0\right)\)

Do đó: ΔAMC=ΔANB

=>MC=BN

Ta có: OM+OC=CM

ON+OB=BN

mà OC=OB và CM=BN

nên OM=ON

Ta có: ΔAMC=ΔANB

=>AM=AN

Xét ΔAMO và ΔANO có

AM=AN

MO=NO

AO chung

Do đó: ΔAMO=ΔANO

=>\(\widehat{AOM}=\widehat{AON}\)

=>OA là phân giác của góc MON

e: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)

nên MN//BC

f: ta có: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra AO là đường trung trực của BC

=>AO\(\perp\)CB

giúp em với ạ, em cần gấp, em cảm ơn nhiều

ol

\(6x=3y=5z\Rightarrow\dfrac{x}{5}=\dfrac{y}{10}=\dfrac{z}{6}\)

Áp dụng t/c dãy tỉ số bằng nhau:

\(\dfrac{x}{5}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{2x}{10}=\dfrac{3y}{30}=\dfrac{z}{6}=\dfrac{2x+3y+z}{10+30+6}=\dfrac{-92}{46}=-2\)

\(\Rightarrow\left\{{}\begin{matrix}x=-2.5=-10\\y=-2.10=-20\\z=-2.6=-12\end{matrix}\right.\)

6x=5y

=>\(\dfrac{x}{5}=\dfrac{y}{6}\)

mà 2x-y=44

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{2x-y}{2\cdot5-6}=\dfrac{44}{4}=11\)

=>\(x=11\cdot5=55;y=11\cdot6=66\)

Ta có AM là tia phân giác của \(\widehat{A}\)

\(\Rightarrow\widehat{BAC}=\widehat{BAM}+\widehat{CAM}=2\cdot\widehat{BAM}\\ \Rightarrow\widehat{BAM}=\dfrac{\widehat{BAC}}{2}=\dfrac{30^0}{2}=15^0\)

Vì ΔABC đều có G là trọng tâm

nên GB=GA=GC

=>\(GB=GC=\dfrac{2}{3}AM=\dfrac{2}{3}\cdot3=2\left(cm\right)\)

Xét ΔABC đều có G là trọng tâm

nên \(GA=GB=\dfrac{2}{3}AM=\dfrac{2}{3}\cdot3=2\left(cm\right)\)

Lời giải:

Nếu $x+y+z=0$

$\Rightarrow \frac{x}{z+y+5}=\frac{y}{x+z+5}=\frac{z}{x+y-10}=0$

$\Rightarrow x=y=z=0$

Nếu $x+y+z\neq 0$

Áp dụng TCDTSBN:

$x+y+z=\frac{x}{z+y+5}=\frac{y}{x+z+5}=\frac{z}{x+y-10}=\frac{x+y+z}{z+y+5+x+z+5+x+y-10}=\frac{x+y+z}{2(x+y+z)}=\frac{1}{2}$

$\Rightarrow \frac{z+y+5}{x}=\frac{x+z+5}{y}=\frac{x+y-10}{z}=2$

$\Rightarrow \frac{x+y+z+5}{x}=\frac{x+y+z+5}{y}=\frac{x+y+z-10}{z}=3$

$\Rightarrow \frac{5,5}{x}=\frac{5,5}{y}=\frac{-9,5}{z}=3$

$\Rightarrow x=\frac{11}{6}; y=y=\frac{11}{6}; z=\frac{-19}{6}$

a.

Do \(\dfrac{a}{b}< \dfrac{c}{d}\Rightarrow ad< bc\Rightarrow ad-bc< 0\)

Ta có:

\(\dfrac{a}{b}-\dfrac{a+c}{b+d}=\dfrac{a\left(b+d\right)-b\left(a+c\right)}{b\left(b+d\right)}=\dfrac{ab+ad-ab-bc}{b\left(b+d\right)}=\dfrac{ad-bc}{b\left(b+d\right)}< 0\)

\(\Rightarrow\dfrac{a}{b}< \dfrac{a+c}{b+d}\)

b.

\(A=\dfrac{a}{a+b+c-c}+\dfrac{b}{a+b+c-a}+\dfrac{c}{a+b+c-b}=\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}\)

\(A>\dfrac{a}{a+b+c}+\dfrac{b}{a+b+c}+\dfrac{c}{a+b+c}\)

\(\Rightarrow A>\dfrac{a+b+c}{a+b+c}\Rightarrow A>1\)

\(A< \dfrac{a+c}{a+b+c}+\dfrac{b+a}{a+b+c}+\dfrac{c+b}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)

\(\Rightarrow1< A< 2\)

\(\Rightarrow\) A nằm giữa 2 số nguyên liên tiếp nên A không phải là số nguyên

3.4 = 6.2

→ 3/6 = 2/4; 3/2 = 6/4; 4/6 = 2/3; 4/2 = 6/3

5.16 = 40.2

→ 5/40 = 2/16; 5/2 = 40/16; 16/40 = 2/5; 16/2 = 40/5