cho tỉ lệ thức a-3/a+3=b-6/b+6 (a không bằng -3, b không bằng -6) tính tỉ số a/b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{2x+3}{5}=\dfrac{y+11}{8}=\dfrac{6x+9}{15}=\dfrac{4y+44}{32}=\dfrac{6x+4y+53}{15+32}=\dfrac{2\left(3x+2y\right)+53}{47}=\dfrac{141}{47}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2x+3}{5}=3\\\dfrac{y+11}{8}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2x+3=15\\y+11=24\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=6\\y=13\end{matrix}\right.\)

\(B=\dfrac{39-\dfrac{6}{5}-\dfrac{3}{7}+\dfrac{3}{11}}{91-\dfrac{14}{5}-1+\dfrac{7}{11}}+\dfrac{\dfrac{5}{3}+\dfrac{15}{11}-3,5}{\dfrac{17}{51}-0,7+\dfrac{3}{11}}\)
\(=\dfrac{3}{7}\cdot\dfrac{\dfrac{7}{3}\cdot\left(39-\dfrac{6}{5}-\dfrac{3}{7}+\dfrac{3}{11}\right)}{91-\dfrac{14}{5}-1+\dfrac{7}{11}}+\dfrac{\dfrac{5}{3}+\dfrac{15}{11}-\dfrac{7}{2}}{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}\)
\(=\dfrac{3}{7}\cdot\dfrac{91-\dfrac{14}{5}-1+\dfrac{7}{11}}{91-\dfrac{14}{5}-1+\dfrac{7}{11}}+5\cdot\dfrac{\dfrac{1}{5}\cdot\left(\dfrac{5}{3}+\dfrac{15}{11}-\dfrac{7}{2}\right)}{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}\)
\(=\dfrac{3}{7}\cdot1+5\cdot\dfrac{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}{\dfrac{1}{3}+\dfrac{3}{11}-\dfrac{7}{10}}\)
\(=\dfrac{3}{7}+5\)
\(=\dfrac{38}{7}\)

a: Xét ΔABC có AB<AC
mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của các cạnh AB,AC
nên \(\widehat{ACB}< \widehat{ABC}\)
b: ta có: ΔAHB vuông tại H
=>AB là cạnh lớn nhất trong ΔABH
=>AB>AH
c: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
=>AB=AD
mà AB<AC
nên AD<AC
d: Xét ΔADC có DC>AC-AD
mà AD=AB
nên DC>AC-AB
=>AC-AB<DC
Khi giải toán hình cần phải có hình vẽ Phước Thịnh nhé

a: Xét ΔBAE và ΔBHE có
BA=BH
\(\widehat{ABE}=\widehat{HBE}\)
BE chung
Do đó: ΔBAE=ΔBHE
=>\(\widehat{BAE}=\widehat{BHE}\)
mà \(\widehat{BAE}=90^0\)
nên \(\widehat{BHE}=90^0\)
=>HE\(\perp\)BC
b: Ta có: ΔBAE=ΔBHE
=>EA=EH
=>E nằm trên đường trung trực của AH(1)
Ta có: BA=BH
=>B nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)(hai góc đối đỉnh)
Do đó: ΔEAK=ΔEHC
d: ta có: AE=EH
mà EH<EC(ΔEHC vuông tại H)
nên AE<EC

a) ĐKXĐ: $x\ne-2$
\(\dfrac{x^4+2x^2+7}{x+2}=\dfrac{x^4+2x^3-2x^3-4x^2+6x^2+12x-12x-24+31}{x+2}\)
\(=\dfrac{x^3\left(x+2\right)-2x^2\left(x+2\right)+6x\left(x+2\right)-12\left(x+2\right)+31}{x+2}\)
\(=\dfrac{\left(x^3-2x^2+6x-12\right)\left(x+2\right)+31}{x+2}\)
\(=x^3-2x^2+6x-12+\dfrac{31}{x+2}\)
b) Đặt \(f\left(x\right)=x^2+10x+a\). Khi đó, vì \(f(x)\vdots(x+3)\) nên theo định lí Bezóut, ta được: \(f\left(-3\right)=0\)
\(\Leftrightarrow\left(-3\right)^2+10\cdot\left(-3\right)+a=0\)
\(\Leftrightarrow-21+a=0\Leftrightarrow a=21\)
b: \(x^2+10x+a⋮x+3\)
=>\(x^2+3x+7x+21+a-21⋮x+3\)
=>a-21=0
=>a=21
a: 

a: Xét ΔADC vuông tại D và ΔAEB vuông tại E có
AC=AB
\(\widehat{DAC}\) chung
Do đó: ΔADC=ΔAEB
b: ta có: ΔADC=ΔAEB
=>AD=AE
Xét ΔADI vuông tại D và ΔAEI vuông tại E có
AI chung
AD=AE
Do đó: ΔADI=ΔAEI
=>\(\widehat{DAI}=\widehat{EAI}\)
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC
c: Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
d: Ta có: ID=IE(ΔADI=ΔAEI)
mà ID<IB(ΔIDB vuông tại D)
nên IE<IB
e: Kẻ EM//AB(M\(\in\)BC)
Ta có: EM//AB
=>\(\widehat{EMC}=\widehat{ABC}\)(hai góc đồng vị)
mà \(\widehat{ABC}=\widehat{ECM}\)(ΔABC cân tại A)
nên \(\widehat{EMC}=\widehat{ECM}\)
=>EM=EC
Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE và AB=AC
nên DB=EC
=>BF=EC
Xét ΔKEM và ΔKFB có
\(\widehat{KME}=\widehat{KBF}\)(hai góc so le trong, BF//ME)
EM=BF
\(\widehat{KEM}=\widehat{KFB}\)(hai góc so le trong, BF//ME)
Do đó: ΔKEM=ΔKFB
=>KF=KE
=>K là trung điểm của EF

Sau 20 phút, lượng nước chảy vào bể là: 20 . 2x = 40x (l)
Sau 20 phút, lượng nước từ bể chảy ra ngoài là: 20x (l)
Biểu thức biểu thị lượng nước trong bể sau khi đồng thời mở các vòi trên sau 20 phút:
150 + 40x - 20x = 150 + 20x (l)

a: Sửa đề: Từ D kẻ DH\(\perp\)AC, chừng minh ΔABD=ΔAHD
Xét ΔABD vuông tại B và ΔAHD vuông tại H có
AD chung
\(\widehat{BAD}=\widehat{HAD}\)
Do đó: ΔBAD=ΔHAD
b: Sửa đề: AD là đường trung trực của BH
Ta có: ΔBAD=ΔHAD
=>BD=HD và BA=HA
Ta có: DB=DH
=>D nằm trên đường trung trực của BH(1)
ta có: AB=AH
=>A nằm trên đường trung trực của BH(2)
Từ (1),(2) suy ra AD là đường trung trực của BH
c: Xét ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
\(\widehat{BDI}=\widehat{HDC}\)(hai góc đối đỉnh)
Do đó: ΔDBI=ΔDHC
=>DI=DC
=>ΔDIC cân tại D

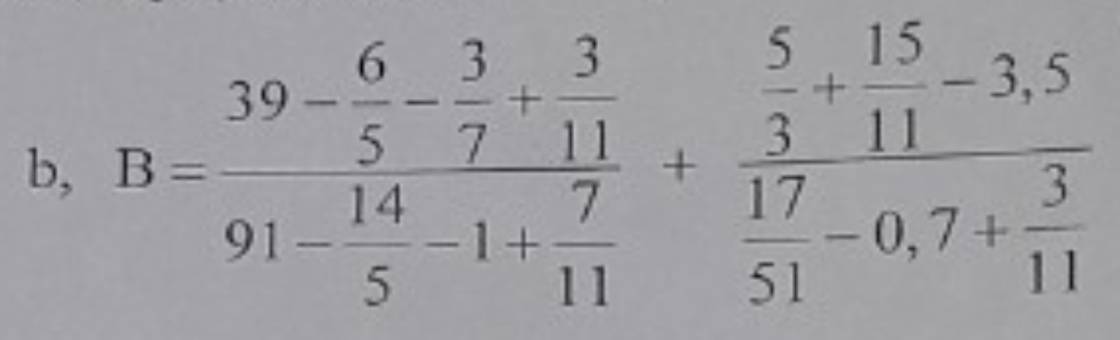

\(\dfrac{a-3}{a+3}=\dfrac{b-6}{b+6}\)
=>(a-3)(b+6)=(a+3)(b-6)
=>\(ab+6a-3b-18=ab-6a+3b-18\)
=>6a-3b=-6a+3b
=>12a=6b
=>\(\dfrac{a}{b}=\dfrac{6}{12}=\dfrac{1}{2}\)