a: Xét ΔABC có D,E lần lượt là trung điểm của AC,AB

=>DE là đường trung bình của ΔABC

=>DE//BC và \(DE=\dfrac{BC}{2}=2\left(cm\right)\)

Xét hình thang BEDC có

M,N lần lượt là trung điểm của EB,DC

=>MN là đường trung bình của hình thang BEDC

=>MN//ED//BC và \(MN=\dfrac{ED+BC}{2}=\dfrac{2+4}{2}=3\left(cm\right)\)

b: Xét ΔBED có MP//ED
nên \(\dfrac{MP}{ED}=\dfrac{BM}{BE}=\dfrac{1}{2}\)

=>\(MP=\dfrac{1}{2}ED=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{4}BC\)

Xét ΔCED có NQ//ED
nên \(\dfrac{NQ}{ED}=\dfrac{CN}{CD}=\dfrac{1}{2}\)

=>\(NQ=\dfrac{1}{2}ED=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{4}BC\)

\(MN=\dfrac{1}{2}\left(ED+BC\right)=\dfrac{1}{2}\left(\dfrac{1}{2}BC+BC\right)=\dfrac{1}{2}\cdot\dfrac{3}{2}BC=\dfrac{3}{4}BC\)

=>\(MP+PQ+QN=\dfrac{3}{4}BC\)

=>\(PQ=\dfrac{3}{4}BC-\dfrac{1}{4}BC-\dfrac{1}{4}BC=\dfrac{1}{4}BC\)

Do đó:MP=PQ=QN

Vậy số thứ hai sẽ bằng 10/100số thứ nhất , số thứ ba sẽ bằng 1/100 số thứ nhất 

Số thứ 3 là :

256,077:(100+10+1)=2,307

Rồi bạn tìm số thứ nhất, thứ hai nhé

Gọi số thập phân cần tìm là \(x\)

Dịch dấu phẩy sang phải tức là tăng \(10\) lần,sang trái tức à giảm \(10\) lần

Theo bài ra ,ta có:

\(x+x\times10+x:10=256,077\)

\(x+x\times10+x\times0,1=256,077\)

\(x\times\left(1+10+0,1\right)=256,077\)

\(x\times11,1=256,077\)

\(x=256,077:11,1\)

\(x=23,07\)

Vậy số cần tìm là \(23,07\)

\(a.4x-6y=2\left(2x-3y\right)\\ b.x^2+6x+9-y^2\\ =\left(x+3\right)^2-y^2\\ =\left(x-y+3\right)\left(x+y+3\right)\\ c.4x^2-9y^2\\ =\left(2x\right)^2-\left(3y\right)^2\\ =\left(2x-3y\right)\left(2x+3y\right)\\ d.x^2-x-y^2+y\\ =\left(x^2-y^2\right)-\left(x-y\right)\\ =\left(x+y\right)\left(x-y\right)-\left(x-y\right)\\ =\left(x-y\right)\left(x+y-1\right)\\ e.x^2-4y^2-6x+9\\ =\left(x^2-6x+9\right)-4y^2\\ =\left(x-3\right)^2-\left(2y\right)^2\\ =\left(x-2y-3\right)\left(x+2y-3\right)\\ f.x^4-y^4+4y^2-4\\ =x^4-\left(y^4-4y^2+4\right)\\ =\left(x^2\right)^2-\left(y^2-2\right)^2\\ =\left(x^2-y^2+2\right)\left(x^2+y^2-2\right)\)

Câu 2: 

\(A=x^2-10x+1\\ =\left(x^2-10x+25\right)-24\\ =\left(x-5\right)^2-24\ge-24\forall x\)

Dấu "=" xảy ra: `x-5=0<=>x=5` 

\(B=x^2-5x+2\\ =\left(x^2-5x+\dfrac{25}{4}\right)-\dfrac{17}{4}\\ =\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2\right)-\dfrac{17}{4}\\ =\left(x-\dfrac{5}{2}\right)^2-\dfrac{17}{4}\ge-\dfrac{17}{4}\forall x\)

Dấu "=" xảy ra: `x-5/2=0<=>x=5/2` 

Câu 2

A = x² - 10x + 1

= x² + 2.x.5 + 25 - 24

= (x + 5)² - 24

Do (x + 5)² ≥ 0 với mọi x ∈ R

⇒ (x + 5)² - 24 ≥ -24 (với mọi x ∈ R)

Vậy GTNN của A là -24 khi x = -5

B = x² - 5x + 2

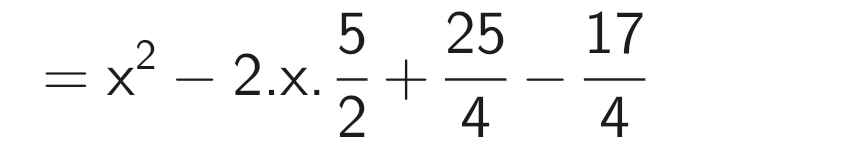
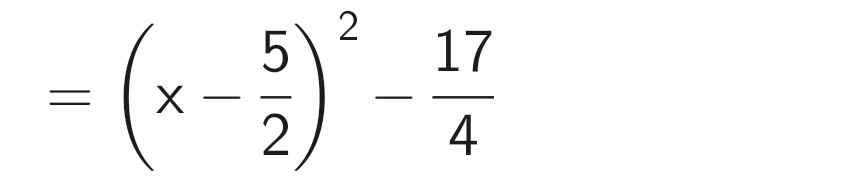
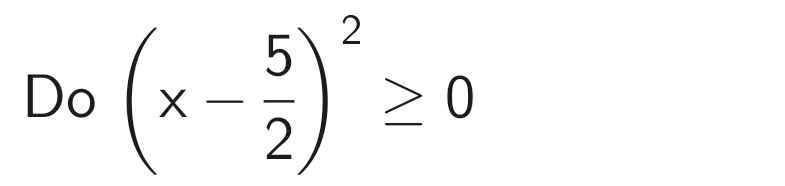
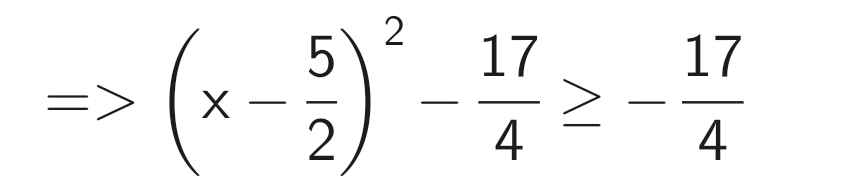
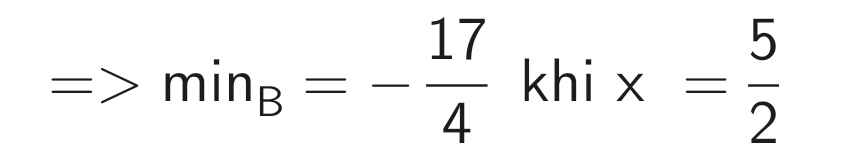
Ta có:

\(\dfrac{43}{41}-1=\dfrac{2}{41};\dfrac{53}{51}-1=\dfrac{2}{51}\)

Vì \(\dfrac{2}{41}>\dfrac{2}{51}\) nên \(\dfrac{43}{41}>\dfrac{53}{51}\)

Lời giải:

Hiệu số thóc của kho A so với kho B: $12\times 2=24$ (tấn)

Nếu chuyển 5 tấn từ B sang A thì hiệu số thóc của kho A so với kho B lúc này:

$24+5\times 2=34$ (tấn) 

Số thóc kho B lúc này: $34:(2-1)\times 1=34$ (tấn) 

Số thóc kho B ban đầu: $34+5=39$ (tấn) 

Số thóc kho A ban đầu: $39+24=63$ (tấn)

Nếu chuyển 12 tấn từ kho A sang kho B thì hai kho bằng nhau tức Kho A hơn kho B số tấn là: 

`12 + 12 = 24` (tấn) 

Nếu chuyển 5 tấn từ kho B sang kho A thì kho A bằng 2 lần kho B tức lúc này kho A hơn kho B số tấn là: 

`24 + 5` x `2 = 34` (tấn)

Ta có sơ đồ: 

Số tấn kho A lúc đó: 2 phần

Số tấn kho B lúc đó: 1 phần

Hiệu số phần bằng nhau là: `2 - 1 = 1` (phần)

Số tấn kho B lúc đó là: `34 : 1` x `1 = 34` (tấn)

Số tấn kho B lúc đầu là: 

`34 + 5 = 39` (tấn) 

Số tấn kho A lúc đầu là: 

`39 + 24 = 63` (tấn)

Đáp số: ....

Bạn xem lại đề, là $13x^3$ hay $13x^2$ vậy?

Biểu thức không có min bạn nhé. Bạn xem lại đề.

Lời giải:

Khi chuyển 5 đơn vị từ mẫu lên tử số thì phân số mới bằng 1, nghĩa là tử số và mẫu số lúc này bằng nhau.

Hiệu của mẫu số và tử số: $5\times 2=10$ 

Nếu chuyển 9 đơn vị từ tử xuống mẫu thì hiệu mẫu và tử số lúc này:

$10+9\times 2=28$ 

Tử số lúc này: $28:(5-3)\times 3=42$

Tử số ban đầu: $42+9=51$

Mẫu số ban đầu: $51+10=61$
Phân số ban đầu: $\frac{51}{61}$

x² + 2y² +3xy - x - y + 3 = 0

(x² - y²) + (3y² + 3xy) - (x + y) = -3

(x - y)(x + y) + 3y(x + y) - (x + y) = -3

(x + y)(x + 2y -1) = -3 = 1.(-3) = (-1).3

(x;y)=(4;-3) (-6;5)