a: Xét ΔNMD vuông tại M và ΔNED vuông tại E có

ND chung

\(\widehat{MND}=\widehat{END}\)

Do đó: ΔNMD=ΔNED
b: Ta có; ΔNMD=ΔNED

=>DM=DE

Xét ΔDMF vuông tại M và ΔDEP vuông tại E có

DM=DE
\(\widehat{MDF}=\widehat{EDP}\)

Do đó: ΔDMF=ΔDEP

=>DF=DP

=>ΔDFP cân tại D

c: Ta có: ΔDMF=ΔDEP

=>MF=EP

ΔNMD=ΔNED
=>NM=NE

Ta có: NM+MF=NF

NE+EP=NP

mà NM=NE và MF=EP

nên NF=NP

=>N nằm trên đường trung trực của FP(1)

Ta có: DF=DP

=>D nằm trên đường trung trực của FP(2)

Ta có: KF=KP

=>K nằm trên đường trung trực của FP(3)

Từ (1),(2),(3) suy ra N,D,K thẳng hàng

ko gửi đc nek.

g. \(-\dfrac{2}{3}\times\dfrac{4}{5}+\dfrac{1}{5}\div\dfrac{9}{11}=-\dfrac{8}{15}+\dfrac{1}{5}\times\dfrac{11}{9}=-\dfrac{8}{15}+\dfrac{11}{45}=\dfrac{24}{45}+\dfrac{11}{45}=\dfrac{35}{45}=\dfrac{7}{9}\)

h.

\(\left(-6,2\div2+3,7\right)\div0,2=\left(-3,1+3,7\right)\div0,2=0,6\div0,2=3\)

k.

\(\dfrac{2}{3}+\dfrac{1}{5}\times\dfrac{10}{7}=\dfrac{2}{3}+\dfrac{10}{35}=\dfrac{2}{3}+\dfrac{2}{7}=\dfrac{14}{21}+\dfrac{6}{21}=\dfrac{20}{21}\)

m.

\(\dfrac{2}{7}+\dfrac{5}{7}\times\dfrac{14}{25}=\dfrac{2}{7}+\dfrac{1\times2}{1\times5}=\dfrac{2}{7}+\dfrac{2}{5}=\dfrac{10}{35}+\dfrac{14}{35}=\dfrac{24}{35}\)

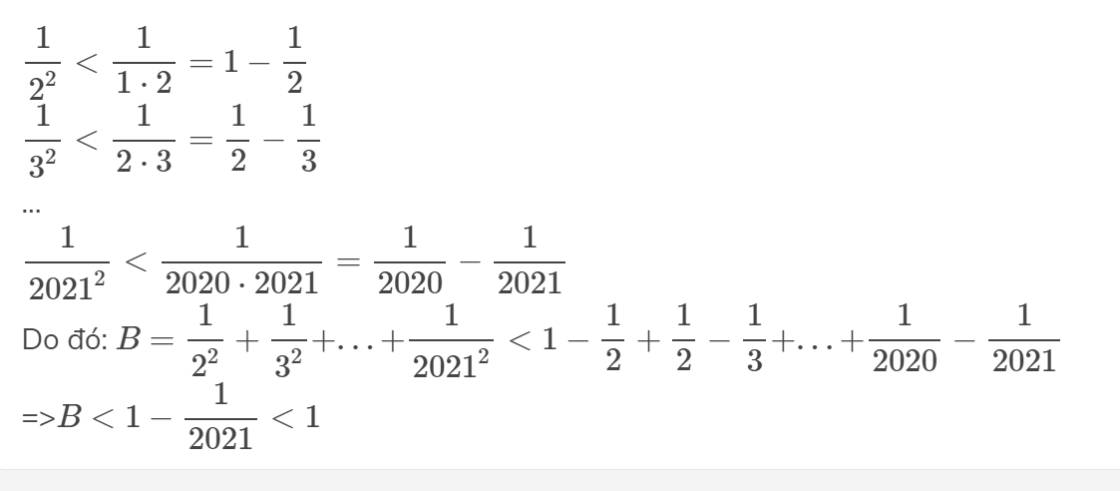
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)

...

\(\dfrac{1}{2021^2}< \dfrac{1}{2020\cdot2021}=\dfrac{1}{2020}-\dfrac{1}{2021}\)

Do đó: \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2021^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\)

=>\(B< 1-\dfrac{1}{2021}< 1\)

LÁ BÀNG

cây bàng

???????????????????.?????????????????????????????????????????????¿??????????????¿????????????????????????????????????

12345678910

a: \(4n-5⋮n\)

=>\(-5⋮n\)

=>\(n\in\left\{1;-1;5;-5\right\}\)

b: \(-11⋮n-1\)

=>\(n-1\inƯ\left(-11\right)\)

=>\(n-1\in\left\{1;-1;11;-11\right\}\)

=>\(n\in\left\{2;0;12;-10\right\}\)

2024 : 14 = 144 dư 8 

A

Bài 5:

a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

=>\(\widehat{ACB}+57^0+72^0=180^0\)

=>\(\widehat{ACB}=51^0\)

Xét ΔABC có \(\widehat{ACB}< \widehat{BAC}< \widehat{ABC}\)

mà AB,BC,AC lần lượt là cạnh đối diện của các góc ACB,BAC,ABC

nên AB<BC<AC

b: Xét ΔBIM và ΔCEM có

MB=MC

\(\widehat{BMI}=\widehat{CME}\)(hai góc đối đỉnh)

MI=ME

Do đó: ΔBIM=ΔCEM

=>\(\widehat{BIM}=\widehat{CEM}\)

=>BI//CE

c: Xét ΔMAK có

MH là đường cao

MH là đường trung tuyến

Do đó: ΔMAK cân tại M

Bài 6:

Số tiền của hóa đơn sau khi giảm giá lần 1 là:

\(16,245:\left(1-5\%\right)=17,1\left(triệuđồng\right)\)

Số tiền đúng của hóa đơn ban đầu là:

17,1:(1-10%)=19(triệu đồng)

Giá niêm yết của cái tivi là:

19-7=12(triệu đồng)