Cho tam giác ABC vuông tại A(AB<AC) có đường cao AH.Gọi I là trung điểm của AC.Kẻ IN vuông góc với BC(M thuộc BC)
a,Chứng minh tam giác ABC đồng dạng với tam giác NIC và CA.CI=CB.CN
b,Chứng minh AB²=BH.BC=NB²-NC²
c,Qua H vẽ đường thẳng vuông góc với AN,đường thẳng này cắt tia AB tại V.Chứng minh B là trung điểm của AV
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Trò chơi
- Điện tử
- Hình thức
- Giải trí
- Lành mạnh
- Hiện nay
- Hiện tượng
- Nghiện
- Vấn đề
- Nghiêm trọng
- Học sinh
- Nghiện (lặp lại)
- Ma túy
- Loại
- Bệnh lý
- Tâm thần
- Tác hại
- Sức khỏe
- Tinh thần

Tỉ số giữa số sách ở ngăn trên lúc đầu so với tổng số sách là \(\dfrac{1}{4+1}=\dfrac{1}{5}\)
Tỉ số giữa số sách ở ngăn trên lúc sau so với tổng số sách là \(\dfrac{1}{5+1}=\dfrac{1}{6}\)
Tổng số sách là \(4:\left(\dfrac{1}{5}-\dfrac{1}{6}\right)=4:\dfrac{1}{30}=120\left(quyển\right)\)

1/3 x 15/13 = 15/39 15/39 : 12/13 = 195/468
195/468 : 7/9 = 1755/3276

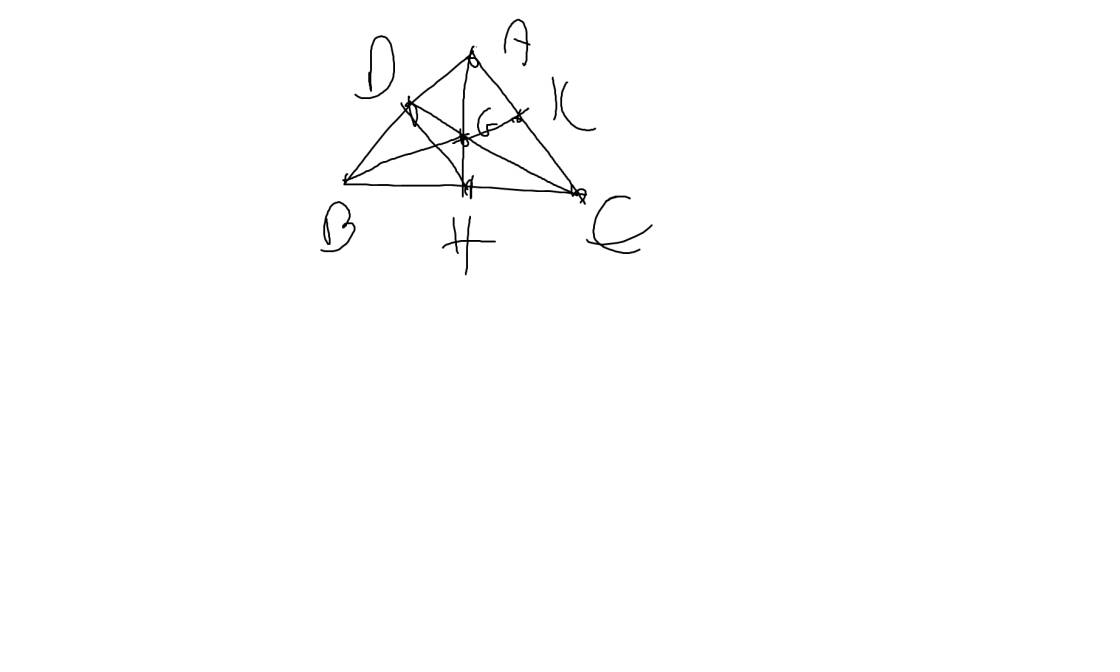
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)
nên \(\widehat{DHA}=\widehat{DAH}\)
=>ΔDAH cân tại D
b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)
\(\widehat{DAH}+\widehat{DBH}=90^0\)
mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DH=DB
=>DA=DB
=>D là trung điểm của AB
Xét ΔABC có
AH,CD là các đường trung tuyến
AH cắt CD tại G
Do đó: G là trọng tâm của ΔABC
c: Xét ΔABC có
G là trọng tâm
Do đó: BG cắt AC tại trung điểm K của AC
TA có:
mà AB=AC
nên AD=DB=AK=KC
Xét ΔDBC và ΔKCB có
DB=KC
BC chung
Do đó: ΔDBC=ΔKCB
=>DC=BK
Xét ΔBAC có
G là trọng tâm
BK là đường trung tuyến
Do đó:
=>2BK=3BG
Trên tia đối của tia KB, lấy E sao cho KB=KE
Xét ΔKAE và ΔKCB có
KA=KC
(hai góc đối đỉnh)
KE=KB
Do đó: ΔKAE=ΔKCB
=>AE=CB
AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)
nên \(\widehat{DHA}=\widehat{DAH}\)
=>ΔDAH cân tại D
b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)
\(\widehat{DAH}+\widehat{DBH}=90^0\)
mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DH=DB
=>DA=DB
=>D là trung điểm của AB
Xét ΔABC có
AH,CD là các đường trung tuyến
AH cắt CD tại G
Do đó: G là trọng tâm của ΔABC
c: Xét ΔABC có
G là trọng tâm
Do đó: BG cắt AC tại trung điểm K của AC
TA có: \(AD=DB=\dfrac{AB}{2}\)
\(AK=KC=\dfrac{AC}{2}\)
mà AB=AC
nên AD=DB=AK=KC
Xét ΔDBC và ΔKCB có
DB=KC
\(\widehat{DBC}=\widehat{KCB}\)
BC chung
Do đó: ΔDBC=ΔKCB
=>DC=BK
Xét ΔBAC có
G là trọng tâm
BK là đường trung tuyến
Do đó: \(\dfrac{BG}{BK}=\dfrac{2}{3}\)
=>2BK=3BG
Trên tia đối của tia KB, lấy E sao cho KB=KE
Xét ΔKAE và ΔKCB có
KA=KC
\(\widehat{AKE}=\widehat{CKB}\)(hai góc đối đỉnh)
KE=KB
Do đó: ΔKAE=ΔKCB
=>AE=CB
AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

TK:
Căn cứ vào đó, trong một số mô hình chăn nuôi bò sữa hiện nay lại cho bò nghe nhạc vì khi cho bò nghe nhạc, bò được thư giãn khiến sản lượng và chất lượng của sữa bò đều tăng.
TK:
Căn cứ vào đó, trong một số mô hình chăn nuôi bò sữa hiện nay lại cho bò nghe nhạc vì khi cho bò nghe nhạc, bò được thư giãn khiến sản lượng và chất lượng của sữa bò đều tăng.

Khi thêm 1 chữ số 0 vào bên phải thì số bé tăng gấp 10 lần
=>Số lớn gấp 10 lần số bé
SỐ lớn là 603:(10-1)x10=603:9x10=670
Số bé là 670-603=67
Số lớn là:
603 : (10 -1) .10 = 670
Số bé là:
670 - 630 = 67
Vậy...
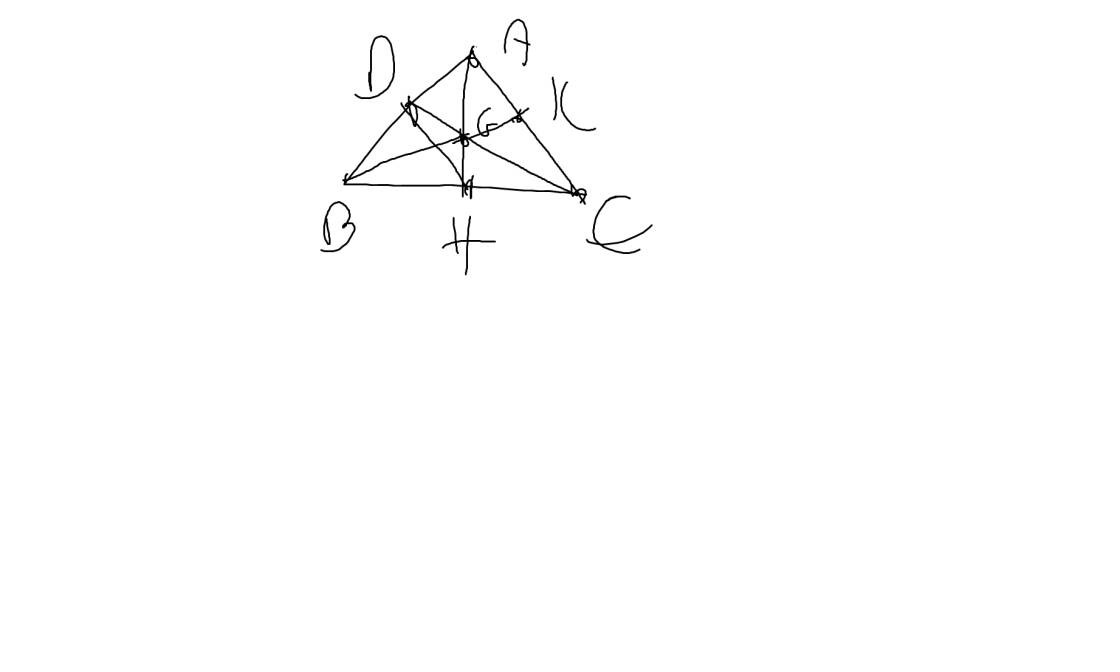
a: Xét ΔCNI vuông tại N và ΔCAB vuông tại A có
\(\widehat{NCI}\) chung
Do đó: ΔCNI~ΔCAB
=>\(\dfrac{CN}{CA}=\dfrac{CI}{CB}\)
=>\(CN\cdot CB=CI\cdot CA\)
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
\(NB^2-NC^2\)
\(=BI^2-IN^2-\left(CI^2-IN^2\right)\)
\(=BI^2-CI^2=BI^2-AI^2=BA^2\)