Bài 4: (1 điểm) Tìm giá trị nhỏ nhất của: $D(x)=2x^2+3 y^2+4 z^2-2(x+y+z)+2$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Gọi I là trung điểm của MC
=>\(MI=IC=\dfrac{MC}{2}\)
mà \(AM=\dfrac{MC}{2}\)
nên AM=MI=IC
Vì AM=MI nên M là trung điểm của AI
Xét ΔBMC có
D,I lần lượt là trung điểm của CB,CM
=>DI là đường trung bình của ΔBMC
=>DI//BM và \(DI=\dfrac{BM}{2}\)
DI//BM nên OM//DI
Xét ΔADI có
M là trung điểm của AI
MO//DI
Do đó: O là trung điểm của AD
b: Xét ΔADI có
O,M lần lượt là trung điểm của AD,AI
=>OM là đường trung bình của ΔADI
=>\(OM=\dfrac{1}{2}DI=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BM=\dfrac{1}{4}BM\)
a: Gọi I là trung điểm của MC
=>��=��=��2MI=IC=MC:2
mà ��=��2AM=MC:2
=> AM=MI=IC
Vì AM=MI => M là trung điểm của AI
Xét ΔBMC có:
D,I lần lượt là trung điểm của CB,CM
=>DI là đường trung bình của ΔBMC
=>DI//BM , ��=��2DI=BM:2
DI//BM => OM//DI
Xét ΔADI có:
M là trung điểm của AI
MO//DI
=> O là trung điểm của AD
b) Xét ΔADI có
O,M lần lượt là trung điểm của AD,AI
=>OM là đường trung bình của ΔADI
=>��=12��=12⋅12⋅��=14��OM=
DI:2=BM:4(đpcm)

a) Gọi A là biến cố "Mặt xuất hiện của xúc xắc là mặt 4 chấm"
P(A) = 22/40 = 11/20
b) Gọi B là biến cố "Mặt xuất hiện của xúc xắc là mặt 6 chấm"
P(B) = 10/18 = 5/9
c) Gọi C là biến cố "Mặt xuất hiện của xúc xắc là mặt 1 chấm"
P(C) = 18/40 = 9/20
d) Gọi D là biến cố "Mặt xuất hiện của xúc xắc là mặt 3 chấm"
P(D) = 14/20 = 7/10
a) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 4 chấm" là 2240= 11204022= 2011.
b) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 6 chấm" là 1840= 9204018= 209.
c) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 1 chấm" là 1440= 7204014= 207.
d) Xác suất thực nghiệm của biến cố "Mặt xuất hiện của xúc xắc là mặt 3 chấm" là 1420= 7102014= 107.

Tổng số học sinh của lớp 8A:
a) Số học sinh Tốt chiếm:
16 . 100% : 40 = 40%
Số học sinh Khá chiếm:
11 . 100% : 40 = 27,5%
b) Số học sinh Chưa đạt chiếm:
3 . 100% : 40 = 7,5%
Do 7,5% > 7% nên cô giáo thông báo tỉ lệ học sinh xếp loại Chưa đạt của lớp chiếm trên 7% là đúng

Gọi vận tốc của xe thứ nhất và xe thứ hai lần lượt là: \(v_1,v_2\)
ĐK: \(v_1,v_2>0\)
Đổi: 1 giờ 20 phút = \(\dfrac{4}{3}\) giờ; 1 giờ 30 pút = \(\dfrac{3}{2}\) (giờ)
Do quãng đường 2 xe đi là bằng nhau nên ta có:
\(\dfrac{4}{3}v_1=\dfrac{3}{2}v_2\Rightarrow8v_1=9v_2\Rightarrow\dfrac{v_1}{9}=\dfrac{v_2}{8}\)
Mỗi giờ xe thứ nhất nhanh hơn xe thứ hai là: \(100\times60=6000\left(m\right)=6\left(km\right)\)
Hay: \(v_1-v_2=6\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{v_1}{9}=\dfrac{v_2}{8}=\dfrac{v_1-v_2}{9-8}=\dfrac{6}{1}=6\)
\(\Rightarrow\dfrac{v_1}{9}=6\Rightarrow v_1=6\cdot9=54\left(km/h\right)\) (tm)
\(\Rightarrow\dfrac{v_2}{8}=6\Rightarrow v_2=8\cdot6=48\left(km/h\right)\) (tm)
Ta có: 1 giờ 20 phút = 80 phút
1 giờ 30 phút = 90 phút
Gọi V1, V2 (m/ phút) lần lượt là vận tốc của xe đi 80 phút và 90 phút.
Vì quãng đường không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên:
Do trong 1 phút xe thứ nhất đi hơn xe thứ hai 100m nên: V1 - V2 = 100
Theo tính chất dãy tỉ số bằng nhau ta có:
V1/90 = 10 ⇒ V1 = 10.90 = 900
V2/80 = 10⇒ V2 = 10.80 = 800
Vậy vận tốc xe thứ nhất V1 = 900(m/phút) = 54(km/h)
Vận tốc xe thứ hai V2 = 800(m/phút) = 48(km/h)
nếu đúng cho mik 1 like nhé!

Câu 1: Đổi 75%=75100=3475%=75100=34
Tổng độ dài của 22 đáy hình thang là:
252×2:12=42 (m)252×2:12=42 (�)
Coi đáy bé là 33 phần bằng nhau thì đáy lớn là 44 phần như thế
Giá trị 11 phần là:
42:(3+4)=6 (m)42:(3+4)=6 (�)
Đáy bé của hình thang là:
6×3=18 (m)6×3=18 (�)
Đáy lớn của hình thang là:
6×4=24 (m)6×4=24 (�)
Đáp số: Đáy bé: 18m18�
Đáy lớn: 24m24�

Dùng phương pháp giải ngược
Giải:
20 trang của quyển truyện ứng với phân số là:
1 - (\(\dfrac{2}{5}\) + \(\dfrac{7}{15}\) + \(\dfrac{2}{3}\)) = - \(\dfrac{8}{15}\) (cuốn truyện)
- \(\dfrac{8}{15}\) < 0
Vậy không có cuốn truyện nào có số trang thỏa mãn đề bài.

Số đinh đã dùng chiếm:
\(\dfrac{5}{6}+\dfrac{1}{4}.\left(1-\dfrac{5}{6}\right)=\dfrac{21}{24}=\dfrac{7}{8}\) (tổng số đinh ốc)
Số đinh ốc chú Toàn có:
\(12:\left(1-\dfrac{7}{8}\right)=12:\dfrac{1}{8}=12.8=96\) (đinh ốc)

12 = 22.3
Ư(12) = {-12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
Lập bảng ta có:
| 2\(x\) + 1 | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | 12 |
| \(x\) | -\(\dfrac{13}{2}\) | -\(\dfrac{7}{2}\) | -\(\dfrac{5}{2}\) | -2 | -\(\dfrac{3}{2}\) | -1 | 0 | \(\dfrac{1}{2}\) | 1 | \(\dfrac{3}{2}\) | \(\dfrac{5}{2}\) | -\(\dfrac{11}{2}\) |
| y - 5 | -4 | -12 | 12 | 4 | ||||||||
| y | 1 | -7 | 17 | 9 | ||||||||
| \(x;y\in\)Z | loại | loại | loại | loại | loại | loại | loại | loại |
Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = (-2; 1); (-1; -7);(0; 17); (1; 9)

P = (a2 + b2) - (10a2 + b2) + 2.(2023b + 3ab)
P = a2 + b2 - 10a2 - b2 + 2.2023b + 2.3ab
P = (a2 - 10a2) + (b2 - b2) + 2.2023.b + 2.3ab
P = -9a2 + 2.2023b + 2.3.ab
P = (-9a2 + 2.3ab) + 2.2023b
P = -3a.(3a - 2b) + 2.2023b (1)
Thay 3a - 2b = 2023 vào (1) ta có:
P = -3a.2023 + 2.2023b
P = -2023.(3a - 2b) (2)
Thay 3a - 2b = 2023 vào (2) ta có:
P = -2023.2023
P = - 20232
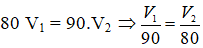
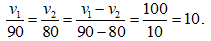
Ta có: \(D\left(x\right)=2x^2+3y^2+4z^2-2\left(x+y+z\right)+2\)
\(=2x^2+3y^2+4z^2-2x-2y-2z+2\)
\(=\left(2x^2-2x\right)+\left(3y^2-2y\right)+\left(4z^2-2z\right)+2\)
\(=2\left(x^2-x\right)+3\left(y^2-\dfrac{2}{3}y\right)+4\left(z^2-\dfrac{1}{2}z\right)+2\)
\(=2\left[x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2\right]+3\left[y^2-2\cdot y\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2-\left(\dfrac{1}{3}\right)^2\right]+4\left[z^2-2\cdot z\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2-\left(\dfrac{1}{4}\right)^2\right]+2\)\(=2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}+3\left(y-\dfrac{1}{3}\right)^2-\dfrac{1}{3}+4\left(z-\dfrac{1}{4}\right)^2-\dfrac{1}{4}+2\)
\(=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+4\left(z-\dfrac{1}{4}\right)^2+\dfrac{11}{12}\)
Mà: \(\left\{{}\begin{matrix}2\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\\3\left(y-\dfrac{1}{3}\right)^2\ge0\forall y\\4\left(y-\dfrac{1}{4}\right)^2\ge0\forall z\end{matrix}\right.\)
\(\Rightarrow D\left(x\right)=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+4\left(z-\dfrac{1}{4}\right)^2+\dfrac{11}{12}\ge\dfrac{11}{12}\forall x,y,z\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y-\dfrac{1}{3}=0\\z-\dfrac{1}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\\z=\dfrac{1}{4}\end{matrix}\right.\)
Vậy: ...
D(x)=2(x2−x)+(3y2−2y)+(4z2−2z)+2
=2(�2−�+14)+3(�2−23�+19)+[(2�)2−2�+14]+2−12−13−14=2(x2−x+41)+3(y2−32y+91)+[(2z)2−2z+41]+2−21−31−41
=2(�−12)2+3(�−13)2+(2�−12)2+112≥112=2(x−21)2+3(y−31)2+(2z−21)2+211≥211
Vậy giá trị nhỏ nhất của �D là: 112211 tại (�,�,�)=(12;13;14)(x,y,z)=(21;31;41).