Số chẵn là gì ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(f\left(x\right)=2x^3+2x+x^2-2x^3-x+1\)
\(=\left(2x^3-2x^3\right)+x^2+2x-x+1=x^2+x+1\)
b: \(h\left(x\right)-f\left(x\right)=2x^2-x-1\)
=>\(h\left(x\right)=2x^2-x-1+x^2+x+1\)
=>\(h\left(x\right)=3x^2\)
c: \(f\left(x\right)\cdot\left(x-1\right)=\left(x^2+x+1\right)\left(x-1\right)\)
\(=x^3-x^2+x^2-x+x-1=x^3-1\)

Bài 2:
a: \(\dfrac{a}{5}=\dfrac{b}{7}\)
mà a-b=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{a-b}{5-7}=\dfrac{10}{-2}=-5\)
=>\(a=-5\cdot5=-25;b=-5\cdot7=-35\)
b: \(\dfrac{a}{-4}=\dfrac{b}{6}=\dfrac{c}{7}\)
mà a-2b+c=18
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{-4}=\dfrac{b}{6}=\dfrac{c}{7}=\dfrac{a-2b+c}{-4-2\cdot6+7}=\dfrac{18}{-9}=-2\)
=>\(\left\{{}\begin{matrix}a=\left(-2\right)\cdot\left(-4\right)=8\\b=-2\cdot6=-12\\c=-2\cdot7=-14\end{matrix}\right.\)
Bài 3:
Gọi độ dài ba cạnh lần lượt là a(cm),b(cm),c(cm)
(Điều kiện: a>0; b>0; c>0)
Độ dài ba cạnh lần lượt tỉ lệ với 3;7;5 nên \(\dfrac{a}{3}=\dfrac{b}{7}=\dfrac{c}{5}\)
Chu vi tam giác là 105cm nên a+b+c=105
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{7}=\dfrac{c}{5}=\dfrac{a+b+c}{3+7+5}=\dfrac{105}{15}=7\)
=>\(a=7\cdot3=21\left(nhận\right);b=7\cdot7=49\left(nhận\right);c=7\cdot5=35\left(nhận\right)\)
Vậy: Độ dài ba cạnh là 21cm; 49cm; 35cm

Bài 6
Em ghi đề sai rồi
Bài 7
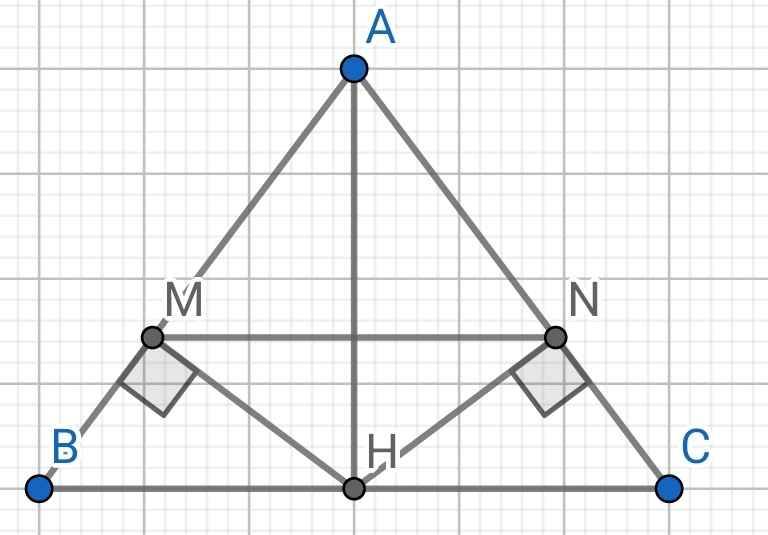
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do H là trung điểm của BC (gt)
⇒ HB = HC
Xét ∆ABH và ∆ACH có:
AB = AC (cmt)
AH là cạnh chung
HB = HC (cmt)
⇒ ∆ABH = ∆ACH (c-c-c)
⇒ ∠BAH = ∠CAH (hai góc tương ứng)
⇒ AH là tia phân giác của ∠BAC
b) Do ∠BAH = ∠CAH (cmt)
⇒ ∠MAH = ∠NAH
Xét hai tam giác vuông: ∆AHM và ∆AHN có:
AH là cạnh chung
∠MAH = ∠NAH (cmt)
⇒ ∆AHM = ∆AHN (cạnh góc vuông - góc nhọn kề)
⇒ AM = AN (hai cạnh tương ứng)
⇒ ∆AMN cân tại A

205: \(f\left(x\right)=x^2-x+1\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)
=>f(x) không có nghiệm thực
204:
a: \(f\left(-1\right)=\left(-1\right)^4+5\cdot\left(-1\right)^3+3\cdot\left(-1\right)^2+2\cdot\left(-1\right)+3\)
\(=1-5+3-2+3\)
=7-7=0
=>x=-1 là nghiệm của f(x)
\(g\left(-1\right)=3\cdot\left(-1\right)^4+\left(-1\right)^3+\left(-1\right)^2-7\cdot\left(-1\right)-10\)
\(=3-1+1+7-10=10-10=0\)
=>x=-1 là nghiệm của g(x)
\(h\left(-1\right)=4\cdot\left(-1\right)^3+2\cdot\left(-1\right)^2-\left(-1\right)+1\)
\(=-4+2+1+1=0\)
=>x=-1 là nghiệm của h(x)


Cho:
| �(�)=P(x)= | 3�23x2 | −3�−3x | +6+6 | |
| �(�)=Q(x)= | 4�34x3 | −5�2−5x2 | +�+x | −3−3 |
Điền hệ số thích hợp vào ô trống.
�(�)+�(�)=P(x)+Q(x)= ((�3x3)) ++ ((�2x2))++ ((�x)) ++ (())
P(x)+Q(x)
\(=3x^2-3x+6+4x^3-5x^2+x-3\)
\(=4x^3-2x^2-2x+3\)

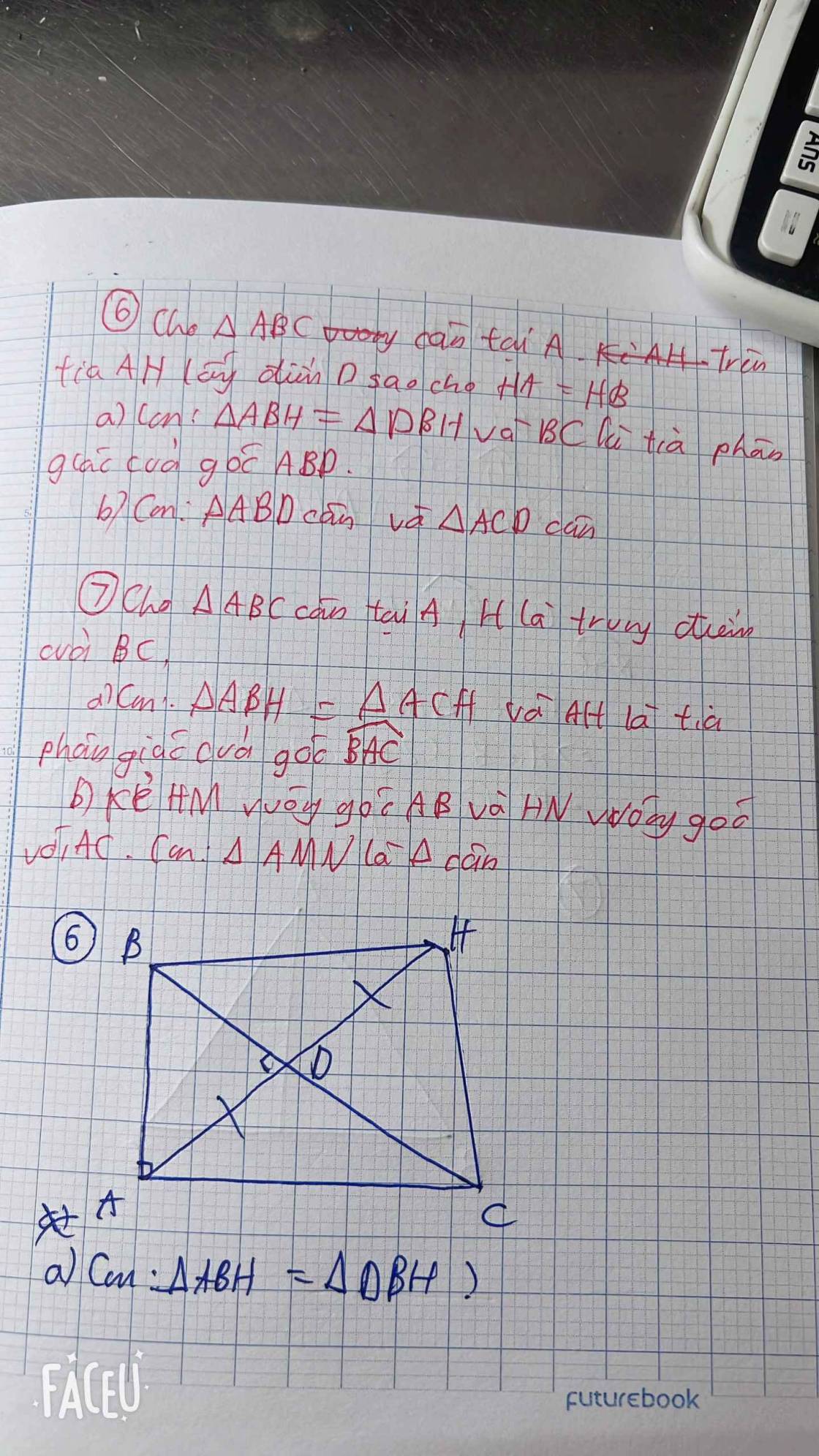
a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
mà \(\widehat{BAH}=\widehat{CKA}\)(hai góc so le trong, BA//CK)
nên \(\widehat{CAK}=\widehat{CKA}\)
=>ΔCAK cân tại C
=>CA=CK
mà CA=BA
nên CK=BA
Ta có: ΔAHB=ΔAHC
=>\(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BC
Ta có: ΔCAK cân tại C
mà CH là đường cao
nên H là trung điểm của AK
Xét ΔBAK có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAK cân tại B
=>BA=BK
c: Đề sai rồi bạn

a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
ta có: ΔABD=ΔACD
=>BD=CD
=>D là trung điểm của BC
mà AD\(\perp\)BC tại D
nên AD là đường trung trực của BC
b:
Cách 1:
XétΔEDB vuông tại D và ΔEDC vuông tại E có
ED chung
DB=DC
Do đó: ΔEDB=ΔEDC
=>EB=EC
=>ΔEBC cân tại E
Cách 2:
Xét ΔEBC có
ED là đường cao
ED là đường trung tuyến
Do đó: ΔEBC cân tại E

a: \(M\left(x\right)=N\left(x\right)+E\left(x\right)\)
=>N(x)=M(x)-E(x)
\(=3x^2+4x+1-x^3+3x^2+3x+1=-x^3+6x^2+7x+2\)
b: \(M\left(1\right)=3\cdot1^2+4\cdot1+1=8\)>0
=>x=1 không là nghiệm của M(x)




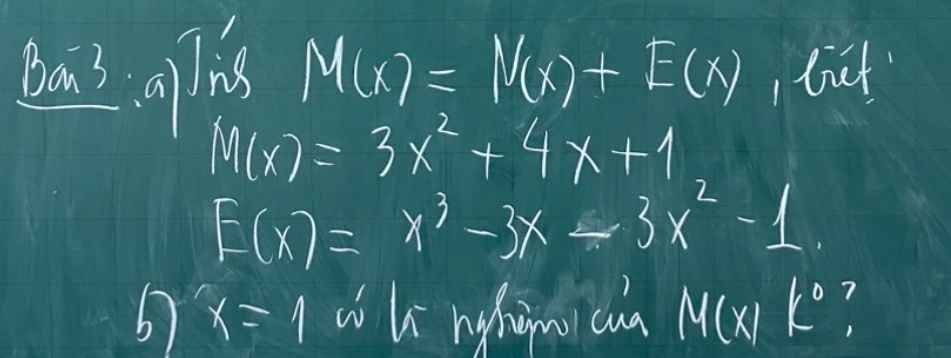
Số chẵn là một số nguyên chia hết cho 2
Cảm ơn bạn nha