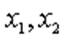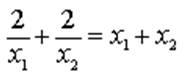. Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax , By lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N. Chứng minh:
1. AC + BD = CD
2. Góc COD = 900
3. AC.BD = 1/4 AB2
4. OC // BM
5. AB là tiếp tuyến của đường tròn đường kính CD.
6. MN vuông góc AB.
7. Xác định vị trí của M để chu vi tứ giác ACDB đạt giá trị nhỏ nhất.