Tìm số tự nhiên x,y thỏa mãn x2 + 2y2 + 2xy + 4y = 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi 15 phút = \(\frac{1}{4}\)giờ
Gọi quãng đường AB là x (km) (x >40)
Thời gian dự định đi hết quãng đường AB là \(\frac{x}{40}\)
Thời gian đi quãng đường còn lại là: \(\frac{x-40}{40+5}=\frac{x-40}{45}\)
Theo đề ra, ta có phương trình:
\(1+\frac{1}{4}+\frac{x-40}{45}=\frac{x}{40}\)
\(\Leftrightarrow\frac{360}{360}+\frac{90}{360}+\frac{8\left(x-40\right)}{360}=\frac{9x}{360}\)
\(\Leftrightarrow360+90+8\left(x-40\right)=9x\)
\(\Leftrightarrow360+90+8x-320=9x\)
\(\Leftrightarrow8x-9x=320-360-90\)
\(\Leftrightarrow-x=-130\)
\(\Leftrightarrow x=130\)(thỏa mãn điều kiện của ẩn)
Vậy quãng đường AB dài 130 km

Gọi tử số là x
Mẫu số là 18 + x
Theo đề ra, ta có phương trình:
\(\frac{x+2}{18+x+2}=\frac{1}{3}\)
\(\Leftrightarrow\frac{x+2}{x+20}=\frac{1}{3}\)
\(\Leftrightarrow3\left(x+2\right)=x+20\)
\(\Leftrightarrow3x+6=x+20\)
\(\Leftrightarrow3x-x=20-6\)
\(\Leftrightarrow2x=14\)
\(\Leftrightarrow x=7\)
Vậy tử số là 7, mẫu số là 18 + 7 = 25 => Phân số ban đầu là: \(\frac{7}{25}\)

\(\frac{36}{x}+\frac{36}{x-12}=\frac{9}{2}\)
ĐKXĐ : x ≠ 0 ; x ≠ 12
pt ⇔ \(36\left(\frac{1}{x}+\frac{1}{x-12}\right)=\frac{9}{2}\)
⇔ \(\frac{x-12}{x\left(x-12\right)}+\frac{x}{x\left(x-12\right)}=\frac{1}{8}\)
⇔ \(\frac{x-12+x}{x\left(x-12\right)}=\frac{1}{8}\)
⇔ \(\frac{2x-12}{x\left(x-12\right)}=\frac{1}{8}\)
⇔ ( 2x - 12 ).8 = x( x - 12 )
⇔ 16x - 96 = x2 - 12x
⇔ x2 - 12x - 16x + 96 = 0
⇔ x2 - 28x + 96 = 0 (1)
Δ' = b'2 - ac = ( b/2 )2 - ac = ( -14 )2 - 96 = 100
Δ' > 0 nên (1) có hai nghiệm phân biệt
\(x_1=\frac{-b+\sqrt{\text{Δ}'}}{a}=\frac{14+\sqrt{100}}{1}=24\)(tm)
\(x_2=\frac{-b-\sqrt{\text{Δ}'}}{a}=\frac{14-\sqrt{100}}{1}=4\)(2)
Vậy phương trình có hai nghiệm x1 = 24 ; x2 = 4
\(\frac{36}{x}+\frac{36}{x-12}=\frac{9}{2}\)ĐKXĐ : \(x\ne0;12\)
\(\Leftrightarrow\frac{72\left(x-12\right)}{2x\left(x-12\right)}+\frac{72x}{2x\left(x-12\right)}=\frac{9x\left(x-12\right)}{2x\left(x-12\right)}\)
Khử mẫu : \(72\left(x-12\right)+72x=9x\left(x-12\right)\)
\(\Leftrightarrow72x-864+72x=9x^2-108x\)
\(\Leftrightarrow252x-864-9x^2=0\)
\(\Leftrightarrow9\left(x-24\right)\left(x-4\right)=0\Leftrightarrow x=24;4\)

Số thứ nhất hơn số thứ hai số đơn vị là:
22 + 13 = 35 ( đơn vị )
Ta có sơ đồ:
Số thứ nhất là:
35 : ( 6-1 ) = 7
Số thứ hai là:
7 x 6 = 42
Đ/s: số thứ nhất 7
số thứ hai 42



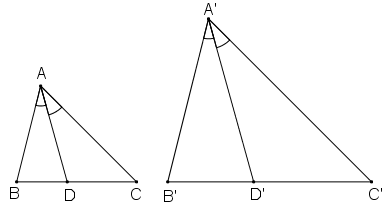
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
( Bạn tự kẻ hình nhé!!! )
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'
Tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k nên:
\(\widehat{B'}=\widehat{B}\), \(\widehat{A'}=\widehat{A}\), \(\frac{A'B'}{AB}=k\)
Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
\(\widehat{B'A'D'}=\frac{1}{2}\widehat{B'A'C'}\), \(\widehat{BAD}=\frac{1}{2}\widehat{BAC}\)
\(\Rightarrow\widehat{B'A'D'}=\widehat{BAD}\)
Xét tam giác A'B'D' và tam giác ABD:
\(\widehat{B'}=\widehat{B}\)
\(\widehat{B'A'D'}=\widehat{BAD}\)
\(\Rightarrow\)tam giác A'B'D' đồng dạng với tam giác ABD
\(\Rightarrow\frac{A'D'}{AD}=\frac{A'B'}{AB}=k\)
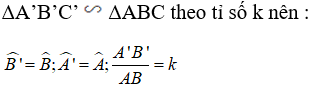
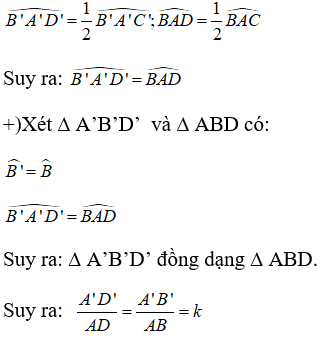
Đề sai ko ạ ? sao ghép như nào cg ko đc ?