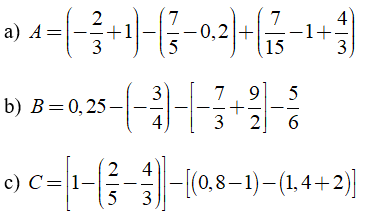Tính giá trị các biểu thức sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|2x-1\right|=\left|x+2\right|\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=x+2\\2x-1=-\left(x+2\right)\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=-\frac{1}{3}\end{cases}}\)

a) \(n^3+2n^2+3n+5=n^3-n^2+3n^2-3n+6n-6+11=\left(n-1\right)\left(n^2+3n+6\right)+11\)
chia hết cho \(n-1\)tương đương \(11⋮\left(n-1\right)\Leftrightarrow n-1\inƯ\left(11\right)=\left\{-11,-1,1,11\right\}\)(vì \(n\)nguyên)
\(\Leftrightarrow n\in\left\{-10,0,2,12\right\}\)
b) \(4n^2+2n+1=4n^2-2n+4n-2+3=\left(2n-1\right)\left(2n+2\right)+3\)chia hết cho \(2n-1\)tương đương với \(3⋮\left(2n-1\right)\Leftrightarrow2n-1\inƯ\left(3\right)=\left\{-3,-1,1,3\right\}\)(vì \(n\)nguyên)
\(\Leftrightarrow n\in\left\{-1,0,1,2\right\}\).
.

Kết luận lại : dạng SHT bằng \(\frac{-628628}{942942}\) là \(\frac{-2}{3}\)

\(\frac{5}{x}+\frac{y}{4}=\frac{1}{8}\)
<=> \(\frac{20+xy}{4x}=\frac{1}{8}\)
<=> 8(20 + xy) = 4x
<=> 2(20 + xy) = x
<=> 40 + 2xy = x
<=> x(1 - 2y) = 40
Lập bảng xét các trường hợp
| x | 1 | 40 | 2 | 20 | 5 | 8 | 10 | 4 | -10 | -4 | -5 | -8 | -2 | -20 | -1 | -40 |
| 1 - 2y | 40 | 1 | 20 | 2 | 8 | 5 | 4 | 10 | -4 | -10 | -8 | -5 | -20 | -2 | -40 | -1 |
| y | -39/2 (loại) | 0 | -19/2(loại) | -1/2(loại) | -7/2 (loại) | -2 | -3/2 (loại) | -9/2(loại) | 5/2(loại) | 11/2(loại) | 9/2(loại) | 3 | 21/2(loại) | 3/2(loại) | 41/2(loại) | 1 |
Vậy các cặp (x;y) tìm được là (40;0) ; (8;-2) ; (-8 ; 3) ; (-40 ; 1)

B = \(\frac{1}{2019}+\frac{2}{2018}+\frac{3}{2017}+\frac{4}{2016}+...+2019\)
\(=\left(\frac{1}{2019}+1\right)+\left(\frac{2}{2018}+1\right)+\left(\frac{3}{2017}+1\right)+\left(\frac{4}{2016}+1\right)+....+1\)
\(=\frac{2020}{2019}+\frac{2020}{2018}+\frac{2020}{2017}+\frac{2020}{2016}+...+\frac{2020}{2020}\)
\(=2020\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{2020}\right)\)
Khi đó \(\frac{A}{B}=\frac{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2020}}{2020\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2020}\right)}=\frac{1}{2020}\)

Có \(5+15=20\), \(2020⋮20\).
Người đầu tiên bốc \(a\)viên thì sau đó người bốc sau bốc \(20-a\)viên. Khi đó số viên bi còn lại luôn là một số chia hết cho \(20\).
Khi đó, số bi cuối cùng sẽ được người bốc sau bốc nên người bốc sau luôn thắng.