Cho a+b+c+d = 0. CMR: a3 +b3+c3+d3 = 3(ab-cd)(c+d)
Giúp mik với ak! Bạn nào trả lời đầu tiên mik sẽ tick nhoa~
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a; \(x^3\) + 64
= \(x^3\) + 43
= (\(x+4\))(\(x^2\) - 4\(x\) + 16)
b; 2\(x^2\) - 4\(x\)
= 2\(x\)(\(x-2\))
c; 6\(x^2\)y + 4\(xy^2\) + 2\(xy\)
= 2\(xy\)(3\(x\) + 2y + 1)
a) x³ + 64
= x³ + 4³
= (x + 4)(x² − 4x + 16)
b) 2x² − 4x
= 2x(x - 2)
c) 6x²y + 4xy² + 2xy
= 2xy(3x + 2y + 1)
d) Sửa đề: x² − x + y − 2xy + y²
= x² − 2xy + y² − x + y
= (x − y)² − (x − y)
= (x − y)(x − y − 1)

A = (\(x+y\))2 - 2.(\(x+y\))z + 4z2
A = (\(x+y\))2 - 2.(\(x+y\))z + (2z)2
A = (\(x+y\) - 2z)2
A = (\(x+y\) - 2z)(\(x+y\) - 2z)

\(D=\dfrac{2^2-1}{2^2}+\dfrac{3^2-1}{3^2}+...+\dfrac{2025^2-1}{2025^2}\)
\(=\left(\dfrac{2^2}{2^2}+\dfrac{3^2}{3^2}+...+\dfrac{2025^2}{2025^2}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=\left(1+1+...+1\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=2024-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+....+\dfrac{1}{2025^2}\right)\)
Đặt \(E=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\)
Do \(E>0\Rightarrow D< 2024\) (1)
Lại có:
\(E< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2024.2025}\)
\(E< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2024}-\dfrac{1}{2025}\)
\(E< 1-\dfrac{1}{2025}< 1\)
\(\Rightarrow D-E>2024-1=2023\) (2)
(1);(2) \(\Rightarrow2023< D< 2024\)
\(\Rightarrow D\) nằm giữa 2 số tự nhiên liên tiếp nên D ko thể là số tự nhiên

\(\Leftrightarrow x^2+2y^2+3xy-4x-5y+3=4\)
\(\Leftrightarrow\left(x^2+2xy-3x\right)+\left(xy+2y^2-3y\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow x\left(x+2y-3\right)+y\left(x+2y-3\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow\left(x+2y-3\right)\left(x+y-1\right)=4\)
Ta có bảng:
| x+2y-3 | -4 | -2 | -1 | 1 | 2 | 4 |
| x+y-1 | -1 | -2 | -4 | 4 | 2 | 1 |
| x | 1 | -3 | -8 | 6 | 1 | -3 |
| y | -1 | 2 | 5 | -1 | 2 | 5 |
Vậy \(\left(x;y\right)=\left(1;-1\right);\left(-3;2\right);\left(-8;5\right);\left(6;-1\right);\left(1;2\right);\left(-3;5\right)\)

1)
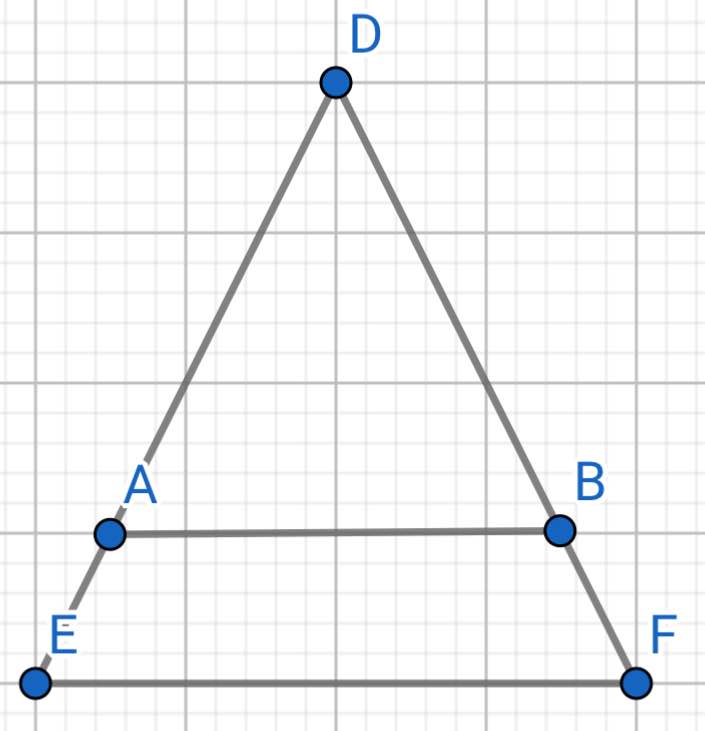
a) Do tam giác DEF cân tại D (gt)
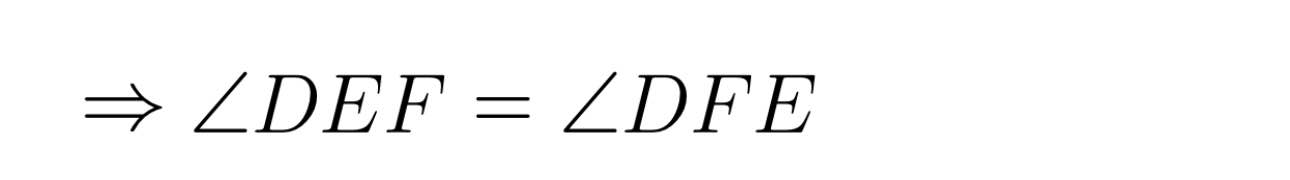
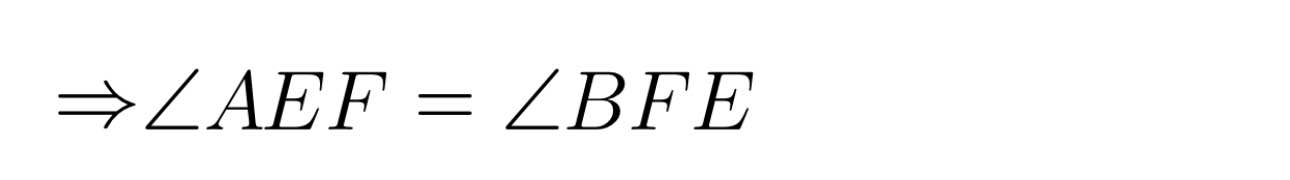
Tam giác DAB có:
DA = DB (gt)
=> Tam giác DAB cân tại D
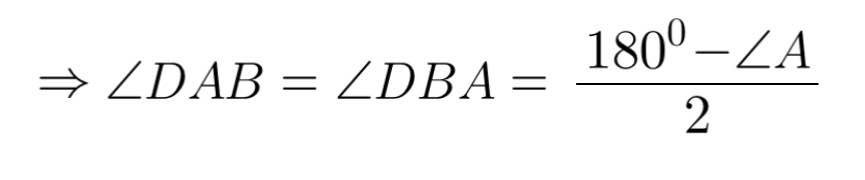
Do tam giác DEF cân tại D (gt)
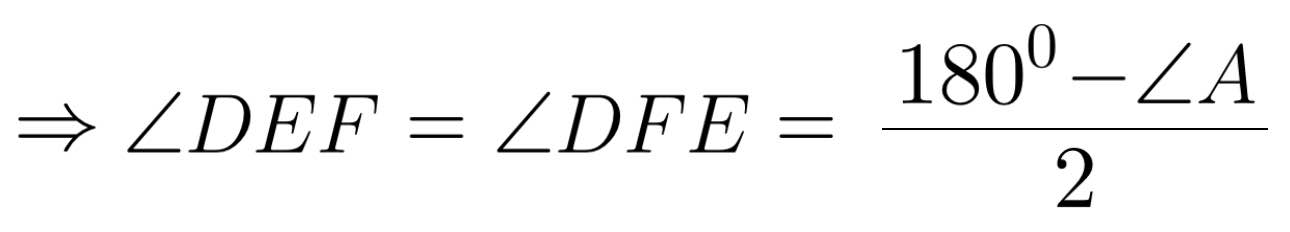
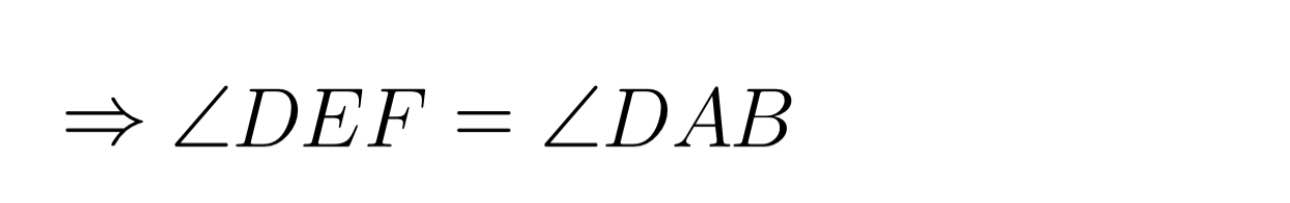
Mà góc DEF và góc DAB đồng vị

=> EABF là hình thang
Mà:
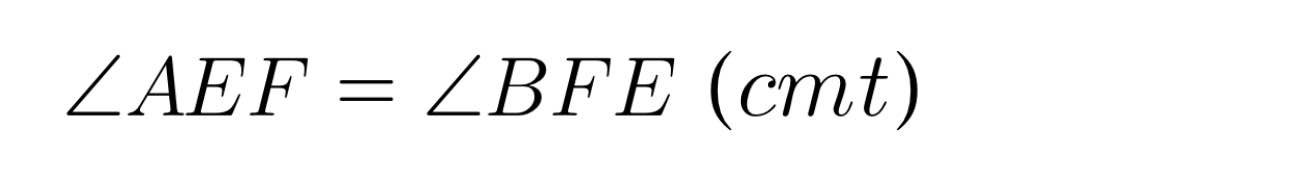
=> EABF là hình thang cân
b) Do tam giác DEF cân tại D (gt)
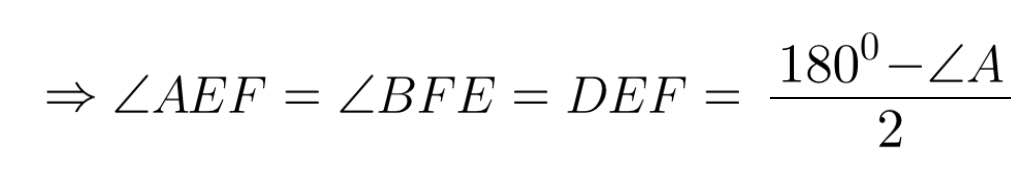
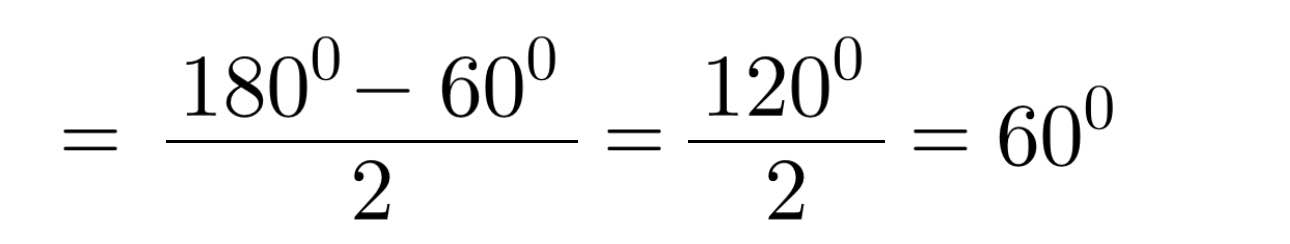
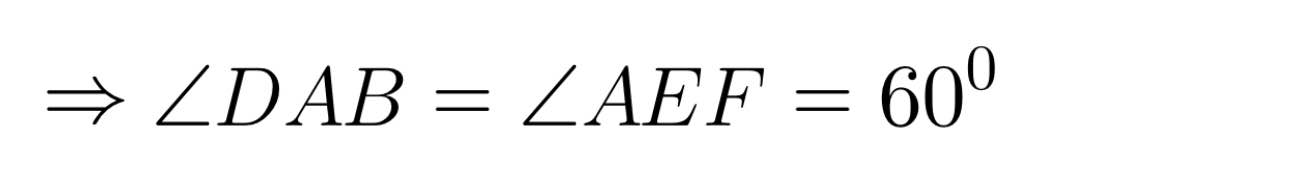
Ta có:
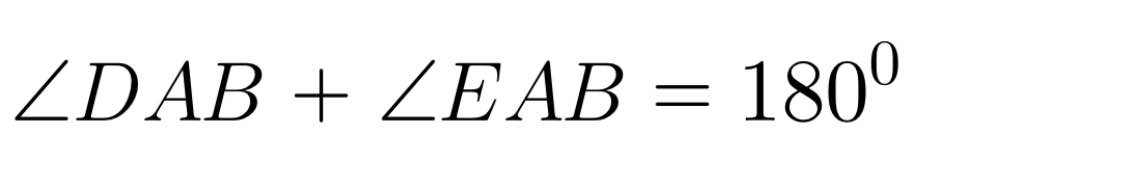
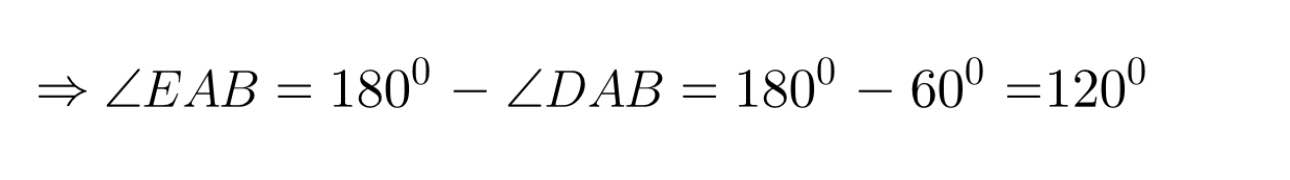

Bài 3
Tam giác ABD có:
AB = AD (gt)
=> Tam giác ABD cân tại A
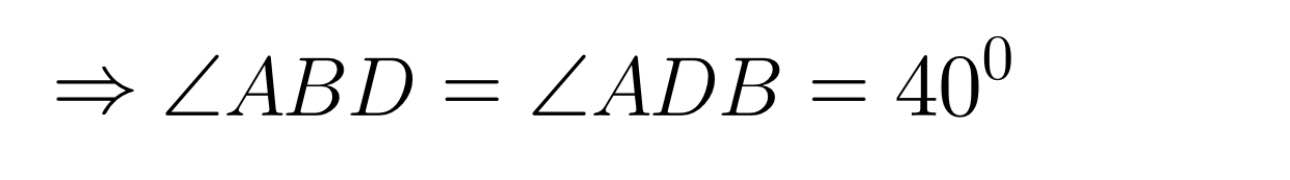
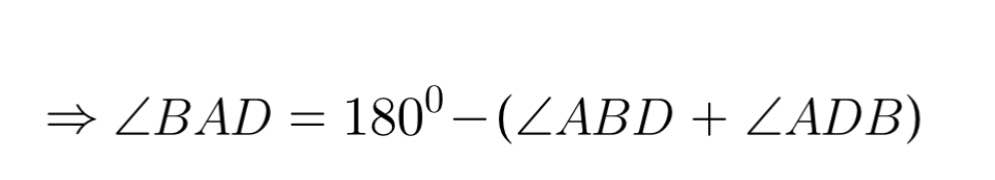
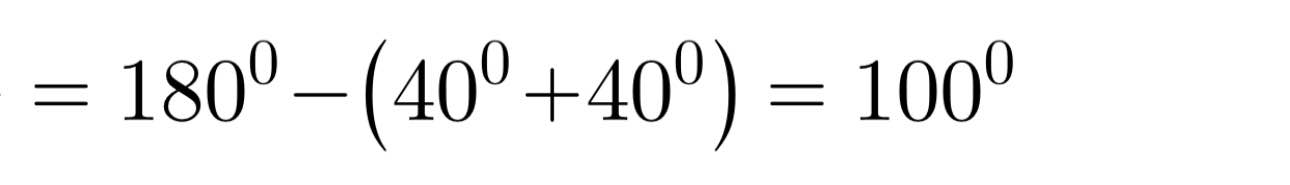
Ta có:
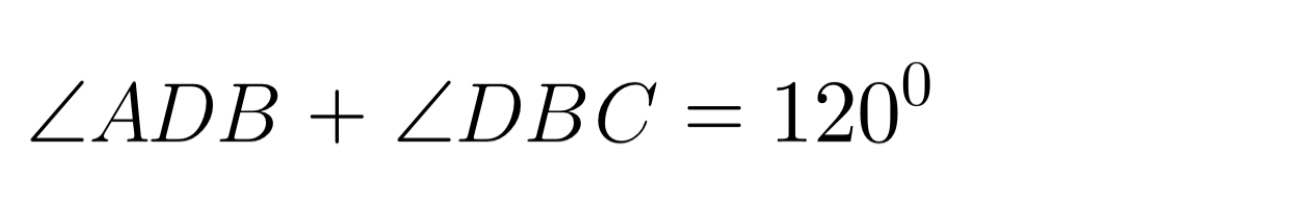
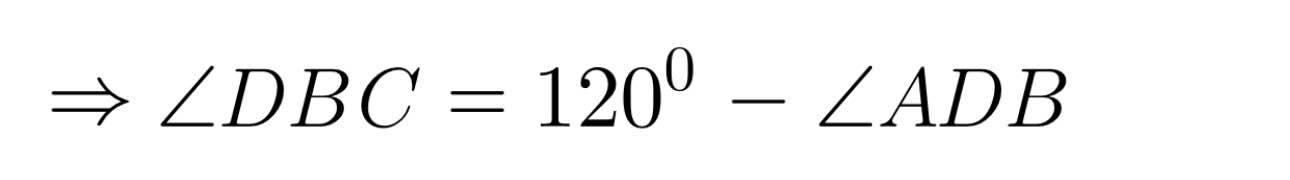
= 120⁰ − 40⁰
= 80⁰
Tam giác BCD có:
CB = CD (gt)
=> Tam giác BCD cân tại C
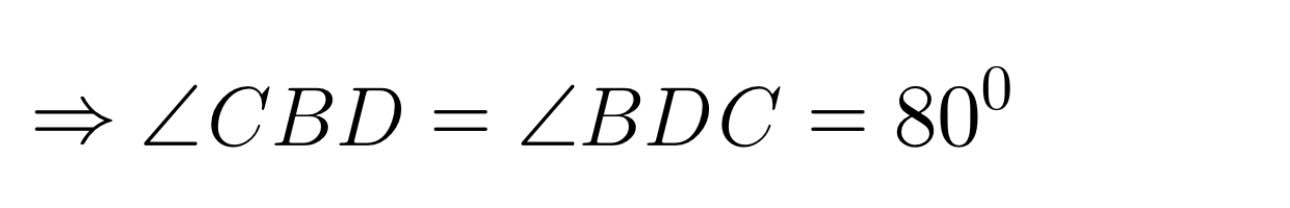
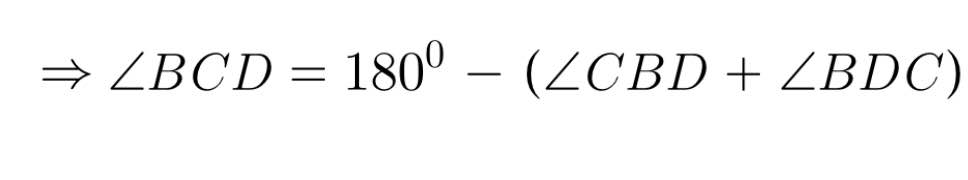
= 180⁰ − (80⁰ + 80⁰) = 20⁰
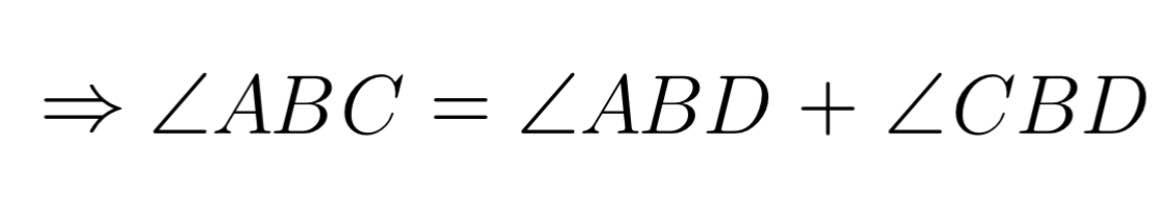
= 40⁰ + 40⁰
= 80⁰

\(P\left(x-1\right)=\left(x^2-2x+1\right)-\left(2x-2\right)+3=\left(x-1\right)^2-2\left(x-1\right)+3\)
\(\Rightarrow P\left(x\right)=x^2-2x+3\)

\(\left(x+1\right)\left(x-1\right)-\left(x+1\right)\\ =x^2-1^2-x-1\\ =x^2-1-x-1\\ =x^2-x-2\)
Phân tích đa thức hay như nào em ơi?
A = (\(x\) + 1)(\(x-1\)) - (\(x+1\))
A = (\(x+1\))(\(x-1\) - 1)
A = (\(x+1\))(\(x\) - 2)
a+b+c+d=0
=>c+d=-(a+b)
\(a^3+b^3+c^3+d^3\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+\left(c+d\right)^3-3cd\left(c+d\right)\)
\(=\left(a+b\right)^3-\left(a+b\right)^3-3ab\left(a+b\right)-3cd\left(c+d\right)\)
=-3ab(a+b)-3cd(c+d)
\(=3ab\left(c+d\right)-3cd\left(c+d\right)=3\left(c+d\right)\left(ab-cd\right)\)