Lượng phần trăm mất đi hay còn lại em ơi?

Luong phan tram mất di á cô

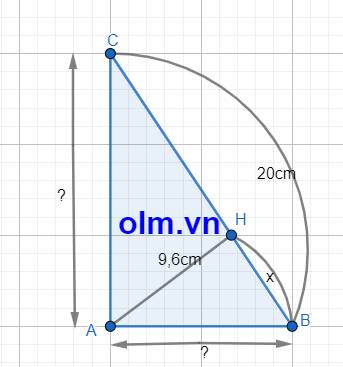
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên  \(x\) < CH

Xét tam giác vuông HAB vuông tại H theo pytago ta có:

AB² = HA² + HB² = 9,6² + \(x^2\) = 92,16 + \(x^2\)

Xét tam giác vuông AHC vuông tại H theo pytago ta có:

AC² = HA² + HC² = 9,6² + (\(20-x\))² = 92,16 + 400 - 40\(x\) + \(x^2\) 

AC² = 492,16 - 40\(x\) + \(x^2\)

Xét tam giác vuông ABC vuông tại A theo pytago ta có:

AC² + AB² = BC²

492,16  - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 20²

(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0

2\(x^2\) - 40\(x\) + 584,32 - 400 = 0

2\(x^2\)- 40\(x\) + 184,32 =0

\(x^2\) - 20\(x\) + 92,16 = 0

△' = 10² - 92,16 = 7,84 > 0

\(x\)₁ =  -(-10) + \(\sqrt{7,84}\) =  12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH  (loại )

\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)

Thay \(x_2\) = 7,2 vào biểu thức: AB² = 92,16 + \(x^2\) = 92,16 + 7,2² = 144 

⇒AB = \(\sqrt{144}\) = 12 

Thay \(x_2\) = 7,2 vào biểu thức: AC² = 492,16 - 40\(x\) + \(x^2\) 

AC² = 492,16 - 40\(\times\) 7,2 + 7,2² = 256

AC = \(\sqrt{256}\) = 16

Kết luận AB = 12 cm; AC = 16 cm 

\(\dfrac{5}{\sqrt{7}}+\sqrt{2}+\dfrac{1}{\sqrt{2}}-1-7+\dfrac{\sqrt{3}}{\sqrt{7}}+1\)

\(=\dfrac{5\sqrt{7}}{7}+\dfrac{3\sqrt{2}}{2}-7+\dfrac{\sqrt{21}}{7}\)

\(=\dfrac{5\sqrt{7}+\sqrt{21}-49}{7}+\dfrac{3\sqrt{2}}{2}\)

\(\dfrac{1}{2\sqrt{3}-3\sqrt{2}}+\dfrac{1}{2\sqrt{3}+3\sqrt{2}}\)

\(=\dfrac{2\sqrt{3}+3\sqrt{2}+2\sqrt{3}-3\sqrt{2}}{\left(2\sqrt{3}-3\sqrt{2}\right)\left(2\sqrt{3}+3\sqrt{2}\right)}\)

\(=\dfrac{\left(2\sqrt{3}+2\sqrt{3}\right)+\left(3\sqrt{2}-3\sqrt{2}\right)}{\left(2\sqrt{3}\right)^2-\left(3\sqrt{2}\right)^2}\)

\(=\dfrac{4\sqrt{3}+0}{4.3-9.2}\)

\(=\dfrac{4\sqrt{3}}{12-18}\)

\(=\dfrac{4\sqrt{3}}{-6}\)

\(=-\dfrac{2\sqrt{3}}{3}\)

\(\dfrac{1}{x}+\dfrac{2}{y}\le1\Rightarrow\dfrac{2}{y}\le1-\dfrac{1}{x}\Rightarrow y\ge\dfrac{2x}{x-1}=2+\dfrac{2}{x-1}\)

\(x+\dfrac{2}{z}\le3\Rightarrow x< 3;\dfrac{2}{z}\le3-x\Rightarrow z\ge\dfrac{2}{3-x}\Rightarrow y+z\ge2+\dfrac{2}{x-1}+\dfrac{2}{3-x}\)

Lúc này ta sẽ áp dụng bất đẳng thức Bunhiacopski

Ta có:

\(6^2\le\left(y+z\right)^2=\left(\sqrt{2}\dfrac{y}{\sqrt{2}}Z\right)^2\le3\left(\dfrac{y^2}{2}+z^2\right)=\dfrac{3}{2}\left(y^2+2z^2\right)\)

\(\Rightarrow P\ge24\). Dấu đẳng thức xảy ra khi và chỉ khi \(y=4,z=2\) 

Vậy giá trị nhỏ nhật của P là 24

Có vẻ bạn bị sai đề bài ở chỗ 4088403 nếu là 4088483 sẽ giải được 

\(A=\dfrac{1}{3}+\dfrac{1}{3.5}+\dfrac{1}{7.5}+\dfrac{1}{7.9}+...+\dfrac{1}{2021.2023}\)

\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)

\(=1-\dfrac{1}{2023}\)

\(=\dfrac{2022}{2023}\)

vậy đây là dang gì hả bạn

Ta có \(p=x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}=2\). Ta đi tìm GTNN của \(B=p+\dfrac{1}{p}\).

Do \(B=\dfrac{p}{4}+\dfrac{1}{p}+\dfrac{3p}{4}\) \(\ge2\sqrt{\dfrac{p}{4}.\dfrac{1}{p}}+\dfrac{3.2}{4}\) \(=\dfrac{5}{2}\). ĐTXR \(\Leftrightarrow\left\{{}\begin{matrix}x=y\\p=2\end{matrix}\right.\) \(\Leftrightarrow x=y=1\).

Vậy GTNN của B là \(\dfrac{5}{2}\) khi \(x=y=1\)

pt đã cho 

\(\Leftrightarrow2x^2-5x+2-\left(x-2\right)\sqrt{x^2-x+1}=0\)

\(\Leftrightarrow\left(x-2\right)\left(2x-1-\sqrt{x^2-x+1}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\2x-1-\sqrt{x^2-x+1}=0\end{matrix}\right.\)

(*) \(2x-1-\sqrt{x^2-x+1}=0\) (đk: \(x\ge\dfrac{2+\sqrt{3}}{4}\))

Ta thấy \(2x-1+\sqrt{x^2-x+1}\ne0\) với mọi \(x\ge\dfrac{2+\sqrt{3}}{4}\), (*) tương đương:

\(\dfrac{\left(2x-1\right)^2-\left(x^2-x+1\right)}{2x-1+\sqrt{x^2-x+1}}=0\)

\(\Leftrightarrow\dfrac{3x\left(x-1\right)}{2x-1+\sqrt{x^2-x+1}}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\\dfrac{3}{2x-1+\sqrt{x^2-x+1}}=0\left(vôlí\right)\end{matrix}\right.\)

Vậy pt đã cho có tập nghiệm \(S=\left\{1;2\right\}\)

Gọi số xe loại một là: \(x\) (chiếc); (\(x\) \(\in\)N*)

Khi đó số xe loại hai là: 50 - \(x\) (chiếc)

Số tiền mua xe loại một là: \(x\) \(\times\) 2 = 2\(x\) ( triệu đồng)

Số tiền mua xe loại hai là: (50 - \(x\)) \(\times\) 6 = 300 - 6\(x\) (triệu đồng)

Theo bài ra ta có phương trình: 2\(x\) + 300 - 6\(x\) = 160

                                                   300 - 4\(x\) = 160

                                                   4\(x\) = 300 - 160

                                                   4\(x\) = 140

                                                      \(x\) = 140 : 4

                                                     \(x\) = 35

Vậy số xe loại một là 35 chiếc

Số xe loại hai là: 50 - 35 =  15 (chiếc)

Kết luận: Cửa hàng đã nhập 35 chiếc xe loại 1 và 15 chiếc xe loại 2