Tìm x,y biết x(x-y) =\(\dfrac{3}{10}\) và y(x-y) = \(\dfrac{-3}{50}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
`255/272 = (15 ×17)/(16×17) = 15/16`
Phân số này vẫn có thể rút gọn nên không phải phân số tối giản

Diện tích thực tế của sân vận động đó là:
0,12x1000=120 (m2)
Đổi : 120 m2=0,012 ha
Đáp số: 0,012 ha

Gọi ƯCLN(n - 1; n - 2) = d; ta có:
\(\left\{{}\begin{matrix}n-1⋮d\\n-2⋮d\end{matrix}\right.\)
n - 1 - (n - 2) ⋮ d
n - 1 - n + 2 ⋮ d
(n - n) + (2 - 1)⋮ d
1 ⋮ d
d = 1
⇒ƯCLN(n - 1; n - 2) = 1
Hay M = \(\dfrac{n-1}{n-2}\) là phân số tối giản (đpcm)
Goi ƯCLN (�−1;�−2)=�⇒�−1:�(n−1;n−2)=d⇒n−1:d và �−2:�n−2:d
⇒(�−1)−(�−2):�⇒1:�⇒(n−1)−(n−2):d⇒1:d
⇒�=1⇒d=1 với mọi �n.
Vậy với mọi �∈�n∈Z thì �=�−1�−2M=n−2n−1 là phân số tối giản.

Bài 1:
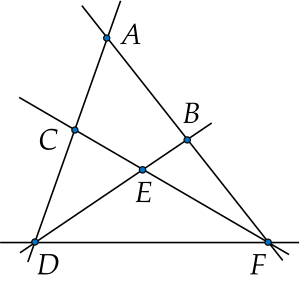
Tên các bộ ba điểm thẳng hàng trong hình vẽ trên lần lượt là:
(A,B,F); (A,C,D); (B,E,D); (C,E,F)
Bài 2:

a; Vì I nằm giữa A và B nên AB = IA + IB
IB = AB - IA = 9 - 4 = 5 (cm)
Kết luận IB = 5 cm
b;

Vì I nằm giữa A và B nên IA và IB là hai tia đối nhau
Mà E là trung điểm IB nên E \(\in\) IB
⇒ IA và IE là hai tia đối nhau nên I nằm giữa A và E
⇒ AE = IA + IE
IE = \(\dfrac{1}{2}\)IB = 5 x \(\dfrac{1}{2}\) = 2,5 (cm)
AE = 4 + 2,5 = 6,5 (cm)
Kết luận AE = 6,5 cm

Bài 1:
2MA = 3MB
⇒ MA = \(\dfrac{3}{2}\)MB
Vì M nằm giữa A và B nên
MA + MB = AB
⇒ \(\dfrac{3}{2}\)MB + MB = AB
\(\dfrac{5}{2}\)MB = AB
MB = AB : \(\dfrac{5}{2}\)
MB = 50 : \(\dfrac{5}{2}\) = 20 (cm)
MA = 50 - 20 = 30 (cm)
Kết luận: MB = 20cm; MA = 30 cm
Bài 2:
3MA = 4MB
MA = \(\dfrac{4}{3}\)MB
Vì M nằm giữa A và B nên
MA + MB = AB
⇒ \(\dfrac{4}{3}\)MB + MB = AB
\(\dfrac{7}{3}\)MB = AB
MB = AB : \(\dfrac{7}{3}\) = 70 : \(\dfrac{7}{3}\) = 30 (cm)
MA = AB - MB = 70 - 30 = 40 (cm)
Kết luận MB = 30 cm; MA = 40 cm

Độ dài của cạnh MC ( hay cạnh MD) là:
30:2=15 (m)
Độ dài của cạnh BC (hay cạnh AD) là:
(102x2):15=13,6 (m)
Diện tích hình thang ABMD là:
(30+15)x13,6:2=306 (m2)
Đáp số: 306 m2

A B C E F H M K D I
a/
E và F bình đẳng nhau nên tôi chỉ c/m ME là tiếp tuyến với đường tròn đường kính AH. Còn c/m MF là tiếp tuyến làm tương tự bạn tự c/m nhé
Gọi I là tâm đường tròng đường kính AH => IA=IH
Gọi D là giao của AH với BC
Xét tg ABC có \(AH\perp BC\) (trong tg 3 đường cao đồng quy)
\(\Rightarrow AD\perp BC\)
Xét tg vuông ADC và tg vuông BEC có
\(\widehat{DAC}=\widehat{EBC}\) (cùng phụ với \(\widehat{C}\) ) (1)
Xét tg vuông AHE có
\(IA=IH\Rightarrow IE=IA=IH=\dfrac{AH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow E\in\left(I\right)\) và tg AIE cân tại I
\(\Rightarrow\widehat{DAC}=\widehat{AEI}\) (góc ở đáy tg cân) (2)
Xét tg vuông BEC có
\(MB=MC\left(gt\right)\Rightarrow ME=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg BME cân tại M
\(\Rightarrow\widehat{EBC}=\widehat{BEM}\) (góc ở đáy tg cân) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{AEI}=\widehat{BEM}\)
Mà \(\widehat{AEI}+\widehat{BEI}=\widehat{AEB}=90^o\)
\(\Rightarrow\widehat{BEM}+\widehat{BEI}=\widehat{MEI}=90^o\Rightarrow ME\perp IE\) => ME là tiếp tuyến với đường tròn đường kính AH
b/
Xét tg MEK và tg MAE có
\(\widehat{AME}\) chung
Ta có
\(sđ\widehat{MEK}=\dfrac{1}{2}sđcungEK\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MAE}=\dfrac{1}{2}sđcungEK\) (góc nội tiếp (O))
\(\Rightarrow\widehat{MEK}=\widehat{MAE}\)
=> tg MEK đồng dạng với tg MAE (g.g.g)
\(\Rightarrow\dfrac{ME}{MA}=\dfrac{MK}{ME}\Rightarrow MK.MA=ME^2\)

\(a^2=bc\)
=>\(\dfrac{a}{b}=\dfrac{c}{a}\)
=>\(\dfrac{a}{c}=\dfrac{b}{a}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{c}=\dfrac{b}{a}=\dfrac{a+b}{a+c}=\dfrac{a-b}{c-a}\)
=>\(\dfrac{a+b}{a+c}=\dfrac{a-b}{c-a}\)
=>\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)



\(x\left(x-y\right)=\dfrac{3}{10}\Rightarrow x-y=\dfrac{3}{10x}\left(1\right)\)
\(y\left(x-y\right)=\dfrac{-3}{50}\Rightarrow x-y=\dfrac{-3}{50y}\left(2\right)\)
Từ (1) và (2) ta có:
\(\dfrac{3}{10x}=\dfrac{-3}{50y}\)
\(\Rightarrow10x=-50y\)
\(\Rightarrow x=-\dfrac{50y}{10}=-5y\)
Thay x = -5y vào (1) ta có:
\(-5y-y=\dfrac{3}{10\cdot-5y}\)
\(\Rightarrow-6y=\dfrac{3}{-50y}\)
\(\Rightarrow300y^2=3\)
\(\Rightarrow y^2=\dfrac{1}{100}\)
\(\Rightarrow y=\pm\dfrac{1}{10}\)
Khi \(y=\dfrac{1}{10}\Rightarrow x=-5\cdot\dfrac{1}{10}=-\dfrac{1}{2}\)
Khi \(y=-\dfrac{1}{10}\Rightarrow x=-5\cdot-\dfrac{1}{10}=\dfrac{1}{2}\)