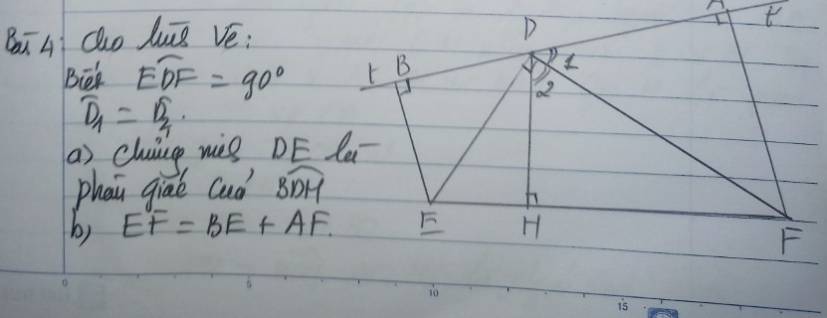
cho hình vẽ: bt EDF = 90 độ
Góc D1 =D2
a) DE LÀ PHÂN GIÁC CỦA GÓC BDM
B) È=BE+AF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(=\frac{7\left(\frac{1}{5}+\frac{1}{11}-\frac{1}{13}+\frac{1}{15}\right)}{3\left(\frac{1}{5}+\frac{1}{13}-\frac{1}{15}+\frac{1}{11}\right)}=\frac{7.\frac{602}{2145}}{3.\frac{646}{2145}}=\frac{7.602}{3.646}=\frac{2107}{969}\)

Theo cm câu b, do \(\Delta BEG=\Delta BFH\Rightarrow EG=FH\) và \(\widehat{BGE}=\widehat{BHF}\)
Hay \(\widehat{IGE}=\widehat{KHF}\)
Do EI vuông góc BG nên tam giác EIG vuông tại I
Do FK vuông góc BH nên tam giác FKH vuông tại K
Xét hai tam giác vuông EIG và FKH có:
\(\left\{{}\begin{matrix}EG=FH\left(cmt\right)\\\widehat{IGE}=\widehat{KHF}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}EIG=\Delta_{\perp}FKH\left(ch-gn\right)\)
\(\Rightarrow EI=FK\)

a: Xét ΔBEF có
BA là đường cao
BA là đường trung tuyến
Do đó: ΔBEF cân tại B
=>BE=BF
b: Xét ΔBGH có
BA là đường cao
BA là đường trung tuyến
Do đó: ΔBGH cân tại B
=>BG=BH
Ta có: AF+FH=AH
AE+EG=AG
mà AF=AE và AH=AG
nên FH=EG
Xét ΔBFH và ΔBEG có
BF=BE
FH=EG
BH=BG
Do đó: ΔBFH=ΔBEG
c: Xét ΔKHF vuông tại K và ΔIGE vuông tại I có
FH=EG
\(\widehat{H}=\widehat{G}\)(ΔBHG cân tại B)
Do đó: ΔKHF=ΔIGE
=>FK=EI

Số học sinh lớp 6B chiếm:
\(\left(1+\dfrac{1}{18}\right)\cdot\dfrac{3}{10}=\dfrac{19}{18}\cdot\dfrac{3}{10}=\dfrac{19}{60}\left(tổngsố\right)\)
Số học sinh lớp 6C chiếm:
\(1-\dfrac{3}{10}-\dfrac{19}{60}=\dfrac{23}{60}\left(tổngsố\right)\)
Hiệu số phần bằng nhau là \(\dfrac{23}{60}-\dfrac{19}{60}=\dfrac{4}{60}=\dfrac{1}{15}\)
Số học sinh lớp 6C là: \(8:\dfrac{1}{15}\cdot\dfrac{23}{60}=46\left(bạn\right)\)
Số học sinh lớp 6B là 46-8=38(bạn)
Số học sinh cả 3 lớp là:
\(46:\dfrac{23}{60}=120\left(bạn\right)\)
Số học sinh lớp 6A là:
120-46-38=36(bạn)
Số học sinh lớp 6A chiếm:
\(\dfrac{36}{120}=30\%\)
Số học sinh lớp 6B chiếm:
\(\dfrac{38}{120}\simeq31,67\%\)
Số học sinh lớp 6C chiếm:
100%-30%-31,67%=38,33%

\(\dfrac{2^{2024}+2^{2023}+2^{2022}+2^{2021}}{60}=\dfrac{2^{2021}\left(2^3+2^2+2+1\right)}{60}=\dfrac{2^{2021}.15}{60}\)
\(=\dfrac{2^{2019}.2^2.15}{60}=\dfrac{2^{2019}.60}{60}=2^{2019}\)
\(\Rightarrow n=2019\)

- Với cửa hàng A:
Giá bán trà sữa từ ly thứ 5 trở đi: \(25000.85\%=21250\) (đồng/ly)
An mua đúng 20 lý nên có 4 ly giá 25000 đồng và 16 ly giá 21250 đồng.
Do đó tổng số tiền phải trả nếu mua ở cửa hàng A là:
\(4.25000+16.21250=440000\) (đồng)
- Với cửa hàng B:
Khi mua 15 ly sẽ được tặng \(15:5=3\) ly, do đó An cần mua thêm 2 ly nữa để đủ 20 ly.
Do đó An cần trả tiền cho \(15+2=17\) ly trà sữa
Số tiền mua ở cửa hàng B là:
\(17.25000=425000\) (đồng)
Vậy An nên mua ở cửa hàng B để tiết kiệm hơn.
Số tiền tiết kiệm được là:
\(440000-425000=15000\) (đồng)

5b.
\(\dfrac{a}{b}>\dfrac{4}{7}\Rightarrow7a>4b\) \(\Rightarrow14a>7a+4b\)
\(\Rightarrow14a>1994\Rightarrow a>\dfrac{997}{7}>142\)
\(\dfrac{a}{b}< \dfrac{2}{3}\Rightarrow2b>3a\Rightarrow4b>6a\) \(\Rightarrow7a+4b>13a\)
\(\Rightarrow13a< 1994\Rightarrow a< \dfrac{1994}{13}< 153\)
\(\Rightarrow142< a< 153\)
Lại có: \(7a+4b=1994\Rightarrow7a-14=1980-4b\)
\(\Rightarrow7\left(a-2\right)=4\left(495-b\right)\)
Do 7 và 4 nguyên tố cùng nhau \(\Rightarrow a-2\) chia hết cho 4 \(\Rightarrow a-2=4k\)
\(\Rightarrow a=4k+2\)
Mà \(142< a< 153\Rightarrow\left[{}\begin{matrix}a=146\\a=150\end{matrix}\right.\)
- Với \(a=146\Rightarrow7.146+4b=1994\Rightarrow b=243\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{146}{243}\)
- Với \(a=150\Rightarrow7.150+4b=1994\Rightarrow b=236\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{150}{236}\)
Vậy phân số cần tìm là \(\dfrac{146}{243}\) hoặc \(\dfrac{150}{236}\)

Gọi số hộp bánh loại I, II, II mà cô Ánh đã mua lần lượt là x;y;z
Do cô mua tổng cộng 54 hộp các loại nên: \(x+y+z=54\)
Số tiền cô mua bánh loại I là: 60x (ngàn)
Số tiền cô mua bánh loại II là: 40y (ngàn)
Số tiền cô mua bánh loại III là: 30z (ngàn)
Do số tiền mua mỗi loại bánh là như nhau nên ta có:
\(60x=40y=30z\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{54}{9}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.6=12\\y=3.6=18\\z=4.6=24\end{matrix}\right.\)
a.
Ta có: \(\widehat{BDE}+\widehat{EDF}+\widehat{D_1}=180^0\)
\(\Rightarrow\widehat{BDE}+90^0+\widehat{D_1}=180^0\)
\(\Rightarrow\widehat{BDE}+\widehat{D_1}=90^0\)
Mà \(\widehat{D_1}=\widehat{D_2}\Rightarrow\widehat{BDE}+\widehat{D_2}=90^0\)
Lại có \(\widehat{HDE}+\widehat{D_2}=\widehat{EDF}=90^0\)
\(\Rightarrow\widehat{BDE}=\widehat{HDE}\)
\(\Rightarrow DE\) là phân giác của \(\widehat{BDH}\)
b.
Xét hai tam giác vuông BDE và HDE có:
\(\left\{{}\begin{matrix}DE-chung\\\widehat{BDE}=\widehat{HDE}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}BDE=\Delta_{\perp}HDE\left(ch-gn\right)\)
\(\Rightarrow BE=HE\)
Tương tự, xét 2 tam giác vuông HDF và ADF có:
\(\left\{{}\begin{matrix}DF-chung\\\widehat{D_2}=\widehat{D_1}\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta_{\perp}HDF=\Delta_{\perp}ADF\left(ch-gn\right)\)
\(\Rightarrow AF=HF\)
\(\Rightarrow HE+HF=BE+AF\)
\(\Rightarrow EF=BE+AF\)