Tổng của ba số bằng 420. Tìm ba số biết số thứ nhất chia cho số thứ hai được thương là 3 và số thứ ba hơn số thứ nhất 14 đơn vị.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. ( 24 x 3 + 56 x 2 ) : ( 96 : 24 )
= ( 72 + 56 x 2 ) : ( 96 : 24 )
= ( 72 + 112 ) : ( 96 : 24 )
= ( 72 + 112 ) : 4
= 184 : 4
= 46
b. 481 : ( 21 + 16 ) x 21
= 481 : 37 x 21
= 13 x 21
= 273

Lời giải:
Gọi số thứ ba là $x$.
Theo bài ra thì:
Số thứ hai là: $2\times x+1$
Số thứ nhất là: $2\times (2\times x+1)+1=4\times x+3$
Tổng ba số: $4\times x+3+2\times x+1+x=123$
$7\times x+4=123$
$7\times x=119$
$x=119:7=17$
Vậy số thứ ba là 17. Số thứ hai là $17\times 2+1=35$. Số thứ nhất là $35\times 2+1=71$

Tổng 3 số là:
75 x 3 = 225
Nếu thêm chữ số 0 vào bên phải số thứ hai thì được số thứ nhất
Do đó nên số thứ nhất gấp 10 lần số thứ hai
Ta có sơ đồ:
Số thứ nhất: |--|--|--|--|--|--|--|--|--|--|
Số thứ hai: |--|
Số thứ ba: |--|--|--|--|
Tổng số phần bằng nhau là:
10 + 1 + 4 = 15 (phần)
Số thứ hai là:
225 : 15 = 15
Số thứ ba là:
15 x 4 = 60
Số thứ nhất là :
15 x 10 = 150

Lời giải:
Diện tích hình vuông ABCD (cũng là hình thoi ABCD) là:
$AC\times BD:2=24$
$AC\times BD=48$
Mà $AC,BD$ đều là đường kính hình tròn nên đặt $AC=BD=2\times r$ với $r$ là bán kính hình tròn. Khi đó:
$2\times r\times 2\times r=48$
$r\times r=48:2:2=12$
Diện tích hình tròn: $3,14\times r\times r= 3,14\times 12=37,68$ (m2)

không có a thích hợp
a x a có những đuôi số (kết quả) là 1, 4, 5; 6, 9
CL thì không
~ hok tốt

An hơn Bình số viên bi là:
15 + 15 = 30 (viên bi)
Ta có sơ đồ số bi của hai bạn:
Bình: |-----|-----| ..... 30 ....
An: |-----|-----|-----|-----|-----|
Hiệu số phần bằng nhau:
5 - 2 = 3 (phần)
Giá trị 1 phần:
30 : 3 = 10 (viên bi)
Số bi của Bình:
10 x 2 = 20 (viên bi)
Số bi của An:
10 x 5 = 50 (viên bi)
An hơn Bình số viên bi là:
15 + 15 = 30 (viên bi)
Ta có sơ đồ số bi của hai bạn:
Bình: |-----|-----| ..... 30 ....
An: |-----|-----|-----|-----|-----|
Hiệu số phần bằng nhau:
5 - 2 = 3 (phần)
Giá trị 1 phần:
30 : 3 = 10 (viên bi)
Số bi của Bình:
10 x 2 = 20 (viên bi)
Số bi của An:
10 x 5 = 50 (viên bi)

Hướng dẫn.
Tính thể tích hộp bánh hình lập phương.
Tính thể tích thùng hình hộp chữ nhật.
Số hộp bánh xếp được: Lấy thể tích thùng : thể tích 1 hộp bánh
Đáp số: 80 hộp bánh
Theo bài ra, ta có sơ đồ: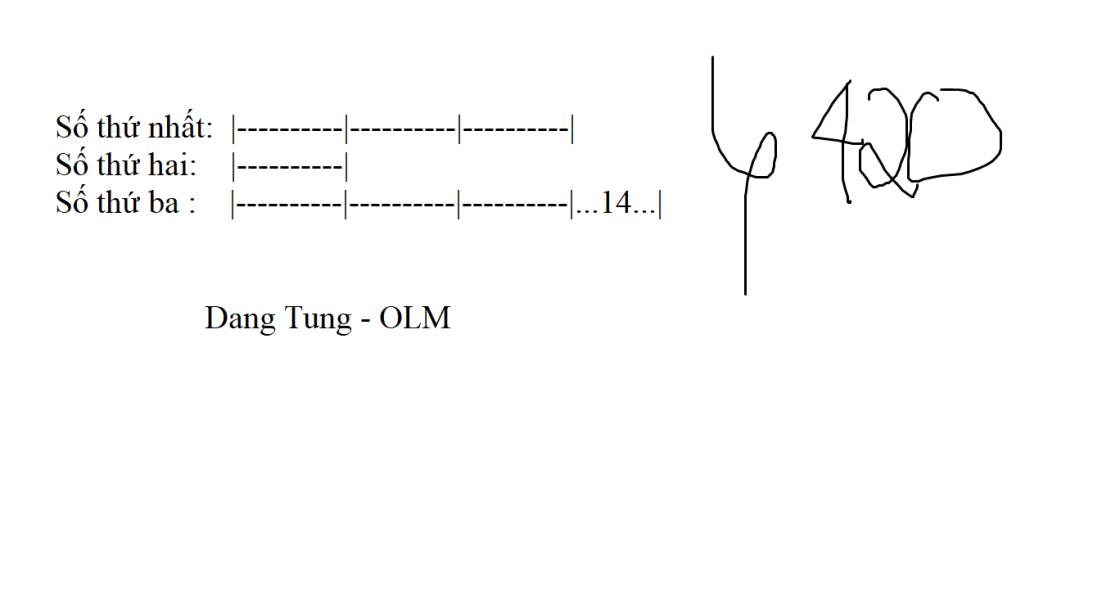 Tổng số phần bằng nhau :
Tổng số phần bằng nhau :
3 + 1 + 3 = 7 (phần)
Giá trị 7 phần:
420 - 14 = 406
Số thứ hai là:
406 : 7 = 58
Số thứ nhất là:
58 x 3 = 174
Số thứ ba là:
174 + 14 = 188