 Giúp mik câu b,c ạ
Giúp mik câu b,c ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$x^3-(x-2)(x^2+x-1)=4(x^2-2)$
$\Leftrightarrow x^3-(x^3+x^2-x-2x^2-2x+2)=4x^2-8$
$\Leftrightarrow x^3-(x^3-x^2-3x+2)=4x^2-8$
$\Leftrightarrow x^3-x^3+x^2+3x-2=4x^2-8$
$\Leftrightarrow x^2+3x-2=4x^2-8$
$\Leftrightarrow 3x^2-3x-6=0$
$\Leftrightarrow x^2-x-2=0$
$\Leftrightarrow (x+1)(x-2)=0$
$\Rightarrow x+1=0$ hoặc $x-2=0$
$\Rightarrow x=-1$ hoặc $x=2$

Lời giải:
1.
$A=3(x-3)+5-2(x-1)=3x-9+5-2x+2=(3x-2x)+(-9+5+2)=x-2=0$
$\Rightarrow x=2$
Vậy $x=2$ là nghiệm của đa thức.
2.
$B=x^2(3x+2)-2x(x-2)=3x^3+2x^2-2x^2+4x=3x^3+4x=x(3x^2+4)=0$
$\Rightarrow x=0$ hoặc $3x^2+4=0$
Nếu $3x^2+4=0$
$\Rightarrow 3x^2=-4<0$ (vô lý)
$\Rightarrow x=0$
Vậy $x=0$ là nghiệm của $B$
3.
$C=x^3+3x(x-2)-x(3x-7)=x^3+3x^2-6x-3x^2+7x=x^3+x=x(x^2+1)=0$
$\Rightarrow x=0$ hoặc $x^2+1=0$
Nếu $x^2+1=0$
$\Rightarrow x^2=-1<0$ (vô lý)
$\Rightarrow x=0$
Vậy $x=0$ là nghiệm duy nhất của $C$.

Lời giải:
a.
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
b.
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.

Câu 1:
a.
$M(x)=2x^3-(x^2+3x^2)+(8-1)=2x^3-4x^2+7$
$N(x)=2x^3-4x^2+3x+(5+7)=2x^3-4x^2+3x+12$
b.
$M(x)+N(x)=(2x^3-4x^2+7)+(2x^3-4x^2+3x+12)$
$=2x^3-4x^2+7+2x^3-4x^2+3x+12=4x^3-8x^2+3x+19$
c.
$3x^2(5x^2-x+2)=3x^2.5x^2-3x^2.x+3x^2.2$
$=15x^4-3x^3+6x^2$
Câu 2:
a.
$A(x)=4x^5+5x^4-(2x^2+x^2)+(7x+x)=4x^5+5x^4-3x^2+8x$
$B(x)=-3x^5-x^4-2x^3+x-2$
b.
$M(x)=A(x)+B(x)=(4x^5+5x^4-3x^2+8x)+(-3x^5-x^4-2x^3+x-2)$
$=4x^5+5x^4-3x^2+8x-3x^5-x^4-2x^3+x-2$
$=(4x^5-3x^5)+(5x^4-x^4)-2x^3-3x^2+(8x+x)-2$
$=x^5+4x^4-2x^3-3x^2+9x-2$
c.
$5x^3(2x^2-3x+10)=5x^3.2x^2-5x^3.3x+5x^3.10$
$=10x^5-15x^4+50x^3$

Bài đã đăng bạn lưu ý không đăng lại nữa nhé, tránh gây loãng box toán.

kết quả thuận lợi cho biến cố "gieo được số chấm lớn hơn 5" là: {mặt 6 chấm}
xác suất để khi "gieo được số chấm lớn hơn 5": 1/6

a) Vì ΔABC cân tại A nên ∠BAC = ∠ABC = 80o. Do đó, ∠BCA = 180o - 2 x 80o = 20o. Vì tam giác ABC cân tại A nên AB = AC.
b) ΔABM và ΔACM có:
∠BAM = ∠CAM (do ∠BAC = ∠ABC)
∠ABM = ∠ACM = 90o (do AM là trung tuyến)
AB = AC (do ΔABC cân tại A) Vậy ΔABM = ΔACM theo nguyên lý góc - cạnh - góc.
c) Để chứng minh AG = 2GM, ta dùng định lý về tỉ số đoạn trên trung tuyến trong tam giác:
Trong ΔABM và ΔACM, ta có ∠BAM = ∠CAM và ∠ABM = ∠ACM. Do đó, ∠BMA = ∠CMA.
Vì BN là trung tuyến của ΔABC, nên BN // AC và BN = \(\dfrac{1}{2}\) AC.
Do đó, ∠BNG = ∠CMA.
Vì ∠BMA = ∠CMA và ∠BNG = ∠CMA, nên ∠BNG = ∠BMA. Do đó, ΔBNG = ΔBMA.
Từ đó, ta có \(\dfrac{BG}{BM}\) = \(\dfrac{NG}{NA}\) = \(\dfrac{1}{2}\), suy ra AG = BG - BA = BG - NG = 2GM.
a, Tam giác ABC cân tại A
=> góc ABC = góc ACB
Xét tam giác ABC cân tại A: góc BAC + góc ABC + góc ACB = 180° (định lí tổng 3 góc trong 1 tam giác)
mà ABC = ACB (cmt)
=> BAC + 2ABC = 180°
⇔ 80° + 2ABC = 180°
2ABC = 100°
ABC = ACB = 50°
So sánh các cạnh của tam giác ABC: AB = AC (tam giác ABC là tam giác cân)
b, Xét tam giác ABM và tam giác ACM:
+ AB = AC (cmt)
+ góc ABC = góc ACB (cmt)
+ BM = CM (AM là đường trung tuyến của tam giác ABC)
=> Tam giác ABM = tam giác ACM (c.g.c) (đpcm)
c, Xét tam giác ABC có hai đường trung tuyến BN và AM cắt nhau tại G (gt)
=> G là trọng tâm của tam giác ABC
=> AG/AM = 2/3; GM/AM = 1/3
=> AG/GM = 2
⇔ AG = 2GM (đpcm)
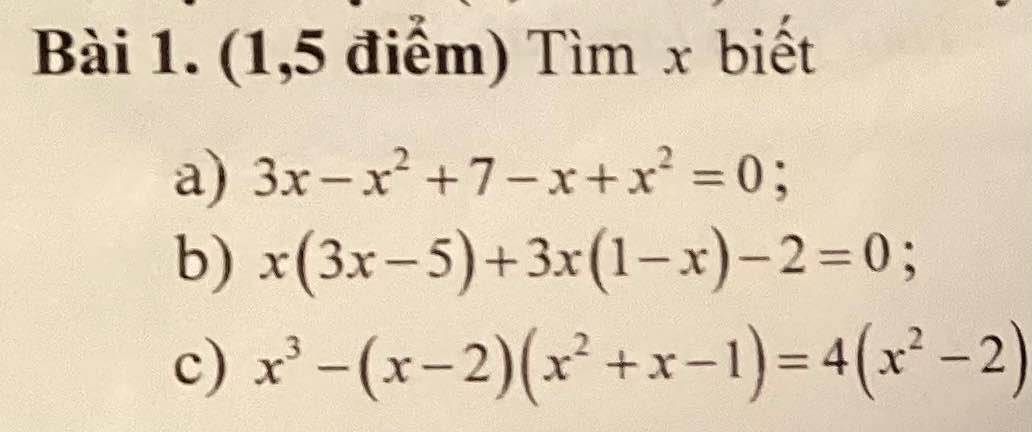






Lời giải:
b.
$(x-1)(x+2)-(x+1)(x-3)-3x=1$
$\Leftrightarrow (x^2+x-2)-(x^2-2x-3)-3x=1$
$\Leftrightarrow x^2+x-2-x^2+2x+3-3x=1$
$\Leftrightarrow 0=0$ (luôn đúng)
Vậy PT có nghiệm $x$ là số thực bất kỳ
c.
$(3x+7)(2x+3)-(3x-5)(2x+11)=0$
$\Leftrightarrow (6x^2+23x+21)-(6x^2+23x-55)=0$
$\Leftrightarrow 76=0$ (vô lý)
Vậy không tồn tại $x$ thỏa mãn đề.