Câu 18. (1 điểm) Tìm giá trị nhỏ nhất của biểu thức $A={{x}^{2}}+2{{y}^{2}}-2xy+2x-6y+2\,028$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TC
38

9 tháng 12 2023
các bạn hướng dẫn mình làm bài 7,8,9 với ạ mình cảm ơn các bạn

AH
Akai Haruma
Giáo viên
8 tháng 12 2023
Lời giải:
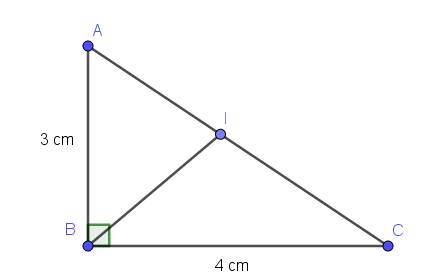
Áp dụng định lý Pitago: $AC=\sqrt{AB^2+BC^2}=\sqrt{3^2+4^2}=5$ (cm)
Áp dụng tính chất tia phân giác:
$\frac{IA}{IC}=\frac{AB}{BC}=\frac{3}{4}$
Mà $IA+IC=AC=5$
$\Rightarrow IA=5:(3+4).3=\frac{15}{7}; IC=5:(3+4).4=\frac{20}{7}$ (cm)



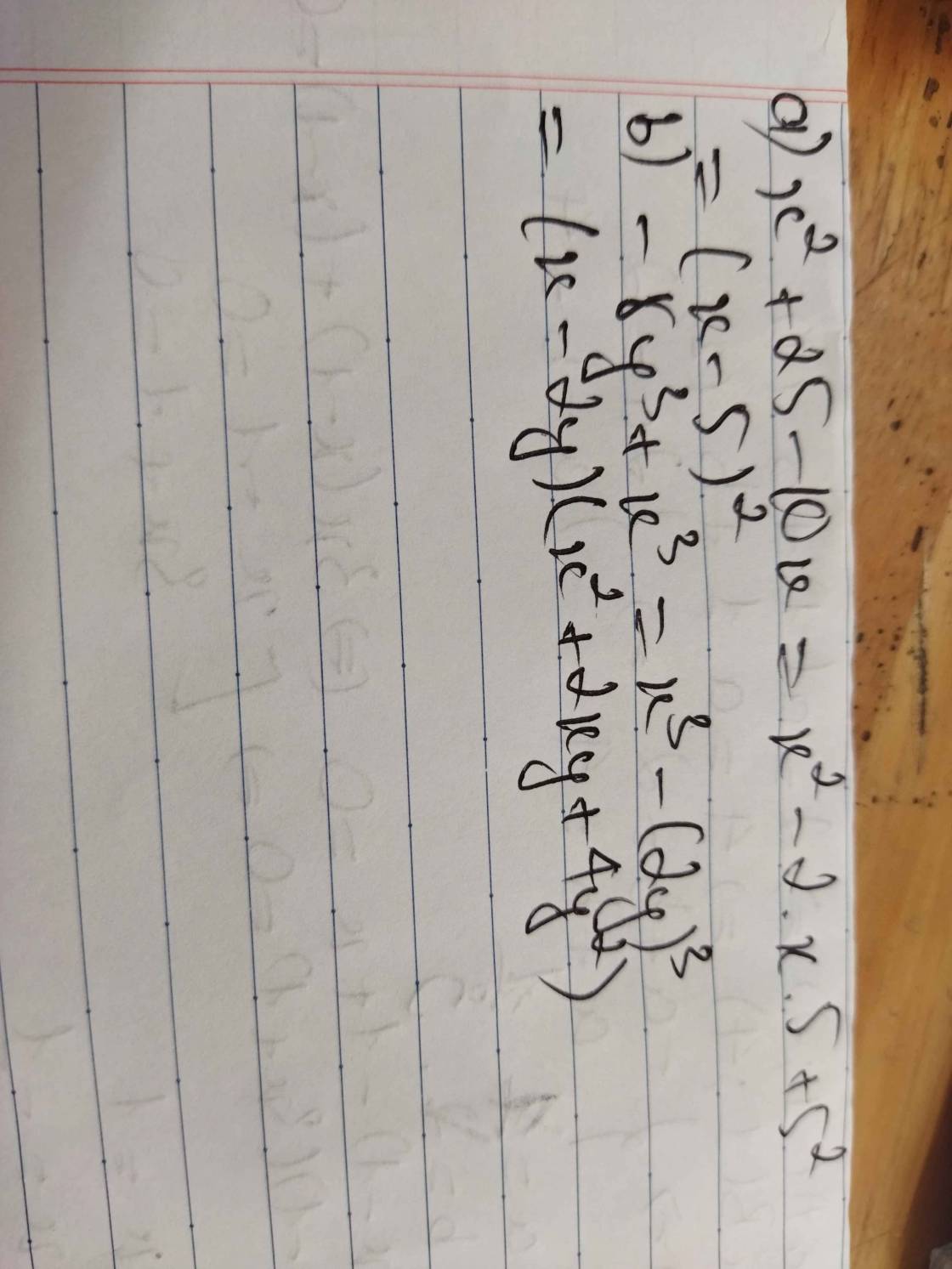
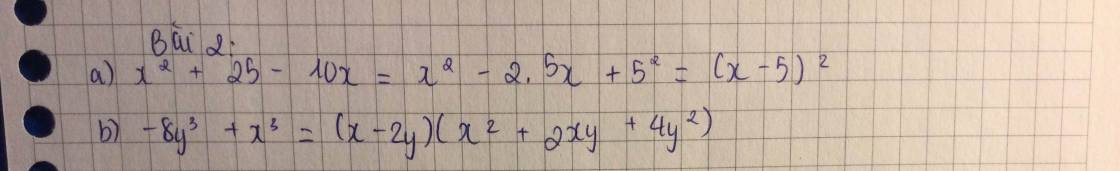

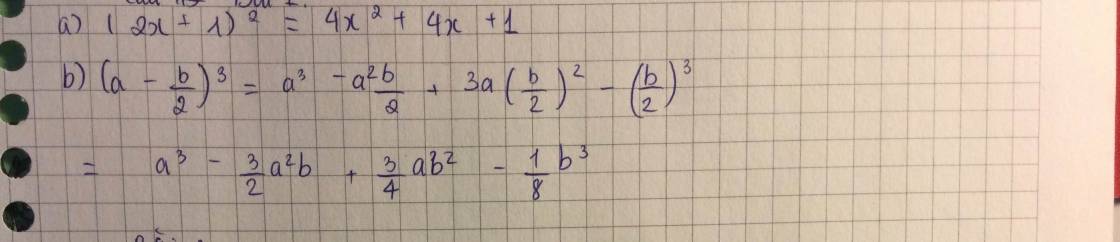

Lời giải:
$A=(x^2-2xy+y^2)+y^2+2x-6y+2028$
$=(x-y)^2+2(x-y)+(y^2-4y)+2028$
$=(x-y)^2+2(x-y)+1+(y^2-4y+4)+2023$
$=(x-y+1)^2+(y-2)^2+2023\geq 0+0+2023=2023$
Vậy $A_{\min}=2023$.
Giá trị này đạt tại $x-y+1=y-2=0$
$\Leftrightarrow y=2; x=1$
A=(x2−2xy+y2)+y2+2x−6y+2028
=(�−�)2+2(�−�)+(�2−4�)+2028=(x−y)2+2(x−y)+(y2−4y)+2028
=(�−�)2+2(�−�)+1+(�2−4�+4)+2023=(x−y)2+2(x−y)+1+(y2−4y+4)+2023
=(�−�+1)2+(�−2)2+2023≥0+0+2023=2023=(x−y+1)2+(y−2)2+2023≥0+0+2023=2023
Vậy �min=2023Amin=2023.
Giá trị này đạt tại �−�+1=�−2=0x−y+1=y−2=0
⇔�=2;�=1⇔y=2;x=1