Gọi vận tốc của ô tô thứ nhất là x(km/h)

(Điều kiện: x>0)

vận tốc của ô tô thứ hai là x+20(km/h)

Thời gian xe ô tô thứ nhất đi từ A đến chỗ gặp là:

10h30p-6h=4h30p=4,5(giờ)

Thời gian xe ô tô thứ hai đi từ A đến chỗ gặp là:

10h30p-7h30p=3(giờ)

Độ dài quãng đường ô tô thứ nhất đi từ A đến chỗ gặp là 

4,5x(km)

Độ dài quãng đường ô tô thứ hai đi từ A đến chỗ gặp là:

3(x+20)(km)

Do đó, ta có phương trình:

4,5x=3(x+20)

=>4,5x=3x+60

=>1,5x=60

=>x=60:1,5=40(nhận)

Vậy: Vận tốc của ô tô thứ nhất là 40km/h

Vận tốc của ô tô thứ hai là 40+20=60km/h

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có

BE chung

BA=BD

Do đó: ΔBAE=ΔBDE

b: Ta có: ΔBAE=ΔBDE

=>\(\widehat{ABE}=\widehat{DBE}\)

Ta có: \(\widehat{BNH}+\widehat{EBC}=90^0\)(ΔBHN vuông tại H)

\(\widehat{AEB}+\widehat{ABE}=90^0\)(ΔABE vuông tại A)

mà \(\widehat{EBC}=\widehat{ABE}\)

nên \(\widehat{BNH}=\widehat{AEB}\)

mà \(\widehat{BNH}=\widehat{ANE}\)(hai góc đối đỉnh)

nên \(\widehat{ANE}=\widehat{AEN}\)

=>ΔANE cân tại A

c: Ta có: ΔBAD cân tại B

mà BE là đường phân giác

nên BE\(\perp\)AD

=>NE\(\perp\)AD

Ta có: ΔANE cân tại A

mà AD là đường cao

nên AD là phân giác của góc NAE

=>AD là phân giác của góc HAC

d: Xét ΔAHD và ΔAED có

AH=AE

\(\widehat{HAD}=\widehat{EAD}\)

AD chung

Do đó: ΔAHD=ΔAED
=>HD=ED và \(\widehat{AHD}=\widehat{AED}\)

Ta có: \(\widehat{AHD}=\widehat{AED}\)

mà \(\widehat{AHD}=90^0\)

nên \(\widehat{AED}=90^0\)

=>DE\(\perp\)AC tại E

=>ΔDEC vuông tại E

=>DE<DC

mà DE=HD

nên HD<DC

e:

Xét ΔABC vuông tại A có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot AH\cdot BC\)

=>\(AB\cdot AC=AH\cdot BC\)

Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

 \(\left(AH+BC\right)^2=AH^2+BC^2+2\cdot AH\cdot BC\)

\(\left(AB+AC\right)^2=AB^2+AC^2+2\cdot AB\cdot AC=BC^2+2\cdot AB\cdot AC\)

mà \(2\cdot AH\cdot BC=2\cdot AB\cdot AC\left(AH\cdot BC=AB\cdot AC\right)\)

nên \(\left(AH+BC\right)^2-\left(AB+AC\right)^2=AH^2>0\)

=>\(\left(AH+BC\right)^2>\left(AB+AC\right)^2\)

=>AH+BC>AB+AC

Có hình không bạn

nếu tất cả các cạnh của hình TG ABC vs hình TG MNP thì diện tích của hình TG MNP bằng ABC

Câu 1:

\(-51\left(15-63\right)-15\left(63-51\right)\)

\(=-51\cdot15+51\cdot63-15\cdot63+51\cdot15\)

\(=51\cdot63-15\cdot63=63\left(51-15\right)=63\cdot36=2268\)

Câu 2:

Sửa đề: \(2n^2+3n-22⋮2n-1\)

=>\(2n^2-n+4n-2-20⋮2n-1\)

=>\(-20⋮2n-1\)

mà 2n-1 lẻ

nên \(2n-1\in\left\{1;-1;5;-5\right\}\)

=>\(n\in\left\{1;0;3;-2\right\}\)

a: Có 7 loại bánh Macaroon

b: Vì 27<34<45<75<78<80

nên loại phô mai nhiều nhất, loại ít nhất là cam

Loại phô mai có nhiều hơn loại cam là:

80-27=53(cái)

c: Để đủ cho mỗi lớp 20 cái thì cần phải có \(20\cdot5=100\left(cái\right)\)

Số cái bánh loại phô mai cần làm thêm là:

100-80=20(cái)

d: Số học sinh khối lớp 1 là:

\(80:\dfrac{1}{2}=160\left(bạn\right)\)

Số học sinh trong 1 lớp là:

160:5=32(bạn)

e: Số cái bánh các vị còn lại là:

34+27+78+45+65+75=324(cái)

bài giải

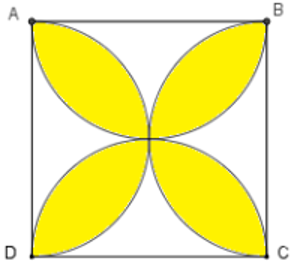
diện tích ABCD là:

4 x 4 = 16 ( cm² )

diện tích hai nữa hình tròn là:

( 4: 2 ) x ( 4 : 2 ) x 3,14 = 12,56 ( cm² )

diện tích phần tô đậm là:

12,56 - ( 16 - 12,56 ) = 12,12 ( cm² )

đáp số: 12,12 cm².

Mười ba phần bốn mươi lăm: 13/45

Bốn phần hai mươi chín: 4/29

13/45

4/29

a) 1 giờ 15 phút + 2 giờ 24 phút + 3 giờ 36 phút

= 1 giờ 15 phút + (2 giờ 24 phút + 3 giờ 36 phút)

= 1 giờ 15 phút + 6 giờ

= 7 giờ 15 phút

b) 2 giờ + 3 giờ + 1 giờ + 4 giờ

= 10 giờ

c) 10 giờ - 5 giờ 25 phút - 2 giờ 35 phút

= 10 giờ - (5 giờ 25 phút + 2 giờ 35 phút)

= 10 giờ - 8 giờ

= 2 giờ

Người đó đến thành phố lúc:

6h30p+1h20p+35p+1h15p

=7h50p+1h50p

=8h100p

=9h40p

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

=>a=bk; c=dk

\(\dfrac{2017a+2018b}{2017a-2018b}=\dfrac{2017\cdot bk+2018b}{2017\cdot bk-2018b}=\dfrac{b\left(2017k+2018\right)}{b\left(2017k-2018\right)}=\dfrac{2017k+2018}{2017k-2018}\)

\(\dfrac{2017c+2018d}{2017c-2018d}=\dfrac{2017\cdot dk+2018d}{2017\cdot dk-2018d}=\dfrac{d\left(2017k+2018\right)}{d\left(2017k-2018\right)}=\dfrac{2017k+2018}{2017k-2018}\)

Do đó: \(\dfrac{2017a+2018b}{2017a-2018b}=\dfrac{2017c+2018d}{2017c-2018d}\)