
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x/y = 0,8 = 4/5
⇒ x/4 = y/5
⇒ 2x/8 = 3y/15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/8 = 3y/15 = (2x + 3y)/(8 + 15) = 46/23 = 2
x/4 = 2 ⇒ x = 2.4 = 8
y/5 = 2 ⇒ y = 2.5 = 10
Vậy x = 8; y = 10

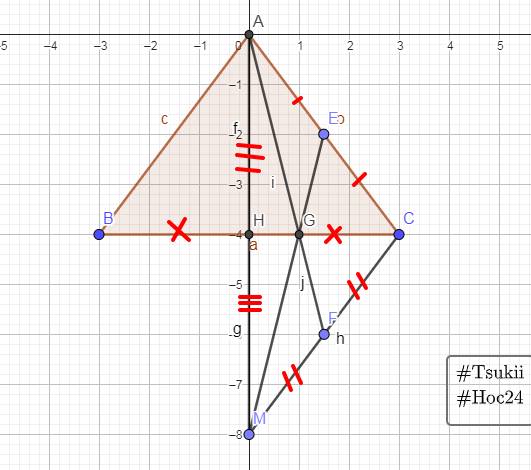
Sửa đề: H là trung điểm của BC
a: Xét ΔAHB và ΔAHC có
AB=AC
AH chung
HB=HC
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔAMH và ΔANH có
AM=AN
\(\widehat{MAH}=\widehat{NAH}\)
AH chung
Do đó: ΔAMH=ΔANH
=>HM=HN
c: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC

Bạn ơi, bạn bổ sung đề trước đi ạ. Đây mới là phần sau của đề thôi

a)Xét 2 tam giác ABH và ACH có:
AB=AC(do tam giác ABC cân tại A)
Góc ABC bằng góc ACB (do tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=>Tam giác ABH = tam giác ACH(cạnh - góc - cạnh)
b)Xét 2 tam giác HBA và HCM có:
Góc AHB bằng góc CHM(2 góc đối đỉnh)
HA=HM(giả thiết)
BH=HC(H là trung điểm BC)
=>Tam giác HBA bằng tam giác HCM(cạnh-góc-cạnh)
=>Góc ABH=góc MCH(2 góc tương ứng)
mà 2 góc này nằm ở vị trí so le trong của đường thẳng AB và MC nên MC//AB
c)Xét tam giác ACM có:
CH là đường trung tuyến(H là trung điểm AM)
AF là đường trung tuyến(F là trung điểm MC)
Mà AF cắt CH tại G(do AF cắt BC tại G;H thuộc BC;G thuộc CH)
=>G là trọng tâm của tam giác ACM
Ta có:
ME cũng là 1 đường trung tuyến của tam giác ACM (E là trung điểm AC)
=>G thuộc ME ( tính chất 3 đường trung tuyến)
=>M,G,E thẳng hàng
`#3107.101107`
`a)`
Vì `\triangle ABC` cân tại A
`\Rightarrow`\(\text{AB = AC; }\widehat{\text{ABC}}=\widehat{\text{ACB}}\)
Xét `\triangle ABH` và `\triangle ACH`:
`\text{AB = AC}`
\(\widehat{\text{ABC}}=\widehat{\text{ACB}}\)
\(\text{HB = HC (H là trung điểm BC)}\)
\(\Rightarrow\) `\triangle ABH = \triangle ACH (c - g - c)`
`b)`
Xét `\triangle AHB` và `\triangle MHC`:
\(\text{AH = HM}\)
\(\widehat{\text{AHB}}=\widehat{\text{MHC}}\left(\text{đối đỉnh}\right)\)
\(\text{HB = HC }\)
`\Rightarrow \triangle AHB = \triangle MHC (c-g-c)`
\(\Rightarrow\widehat{\text{ABH}}=\widehat{\text{MCH}}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí sole trong
\(\Rightarrow\text{ }\text{MC // AB (tính chất)}\)
`c)`
Vì E là trung điểm của AC; F là trung điểm của MC
\(\Rightarrow\text{EA = EC; FM = FC}\)
Ta có:
\(\left\{{}\begin{matrix}\text{EA = EC}\\\text{FM =FC}\\\text{HA = HM}\end{matrix}\right.\)
\(\Rightarrow\text{AF; ME và CH}\) lần lượt là các đường trung tuyến của `\triangle ACM`
Mà AF cắt HC tại G
\(\Rightarrow\) G là trọng tâm của `\triangle ACM`
\(\Rightarrow\) \(\text{G}\in\text{ME}\)
\(\Rightarrow\) `3` điểm M, G, E thẳng hàng (đpcm).

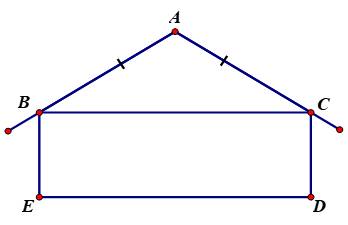
Trong tam giác ABC, áp dụng định lý về tổng 3 góc:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\Leftrightarrow120^0+2.\widehat{ABC}=180^0\) (do \(\widehat{ABC}=\widehat{ACB}\))
\(\Leftrightarrow\widehat{ABC}=30^0\)
Vậy góc tạo bởi mái nhà AB và vách tường BE là:
\(180^0-\left(\widehat{ABC}+\widehat{EBC}\right)=180^0-\left(30^0+90^0\right)=60^0\)

Gọi A là biến cố "Số xuất hiện trên thẻ được rút ra là số chia 4 dư 2"
=>A={2;6;10;14;18;22;26;30}
=>n(A)=8
\(n\left(\Omega\right)=30-1+1=30\)
\(P_A=\dfrac{8}{30}=\dfrac{4}{15}\)
Bài 4:
a) Biến cố "Gieo được mặt có số chấm lẻ" là biến cố không xảy ra
b) Biến cố "Gieo được mặt có số chấm là số chính phương" là biến cố xảy ra
c) Biến cố "Mặt bị úp xuống có 3 chấm" là biến cố xảy ra
Bác Tư có ba tờ giấy bạc loại 20 000 đồng và tờ giấy bạc loại 10 000 đồng . Bác mua gạo hết 50 000 đồng . Số tiền còn dư là