câu d (x-y)² nha mn

Chọn C

a: Xét ΔMAB và ΔMCD có

MA=MC

\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)

MB=MD

Do đó: ΔMAB=ΔMCD

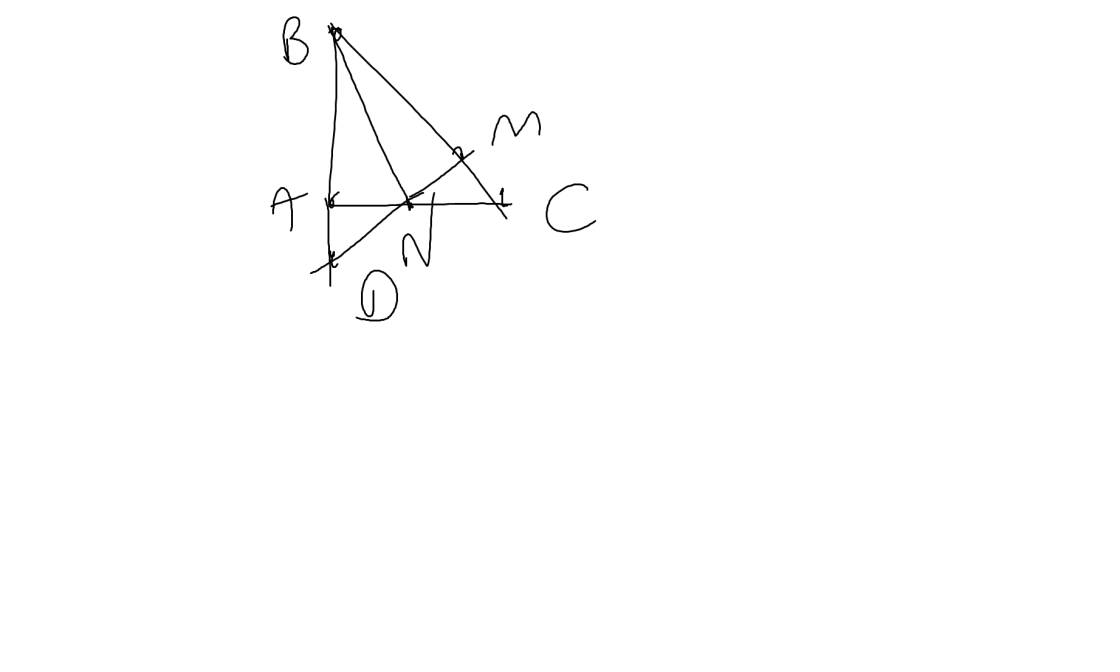
b: Xét ΔCBD có

CM,DN là các đường trung tuyến

CM cắt DN tại G

Do đó: G là trọng tâm của ΔCDB

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=90^0-60^0=30^0\)

b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

BA=BH

Do đó: ΔBAE=ΔBHE

=>\(\widehat{ABE}=\widehat{HBẺ}\)

=>BE là phân giác của góc ABC

c: Xét ΔBKC có

KH,CA là các đường cao

KH cắt CA tại E

Do đó: E là trực tâm của ΔBKC

=>BE\(\perp\)KC

a) Tính góc C: Vì tam giác ABC vuông tại A và góc B = 60 độ, ta có góc C = 90 - 60 = 30 độ.

b) Chứng minh BE là tia phân giác của góc B: Gọi I là trung điểm của AB, vậy BI là đoạn thẳng phân giác của góc B. Ta có HB = AB và BI là đoạn thẳng phân giác của góc B, do đó tam giác BHI là tam giác đều. Do đó, góc BHI = 60 độ. Mà góc HBE là góc ngoài của tam giác BHI, vậy góc HBE = 60 độ. Vậy, BE là tia phân giác của góc B.

c) Chứng minh rằng BE vuông góc với KC: Ta có:

• Tam giác ABC vuông tại A.
• Tam giác BHI đều. Vậy ta có:
• AH là đường cao của tam giác ABC, vì vậy HK là đường cao của tam giác BHI.
• BK là cạnh của tam giác BHI. Vậy tam giác BKH là tam giác vuông tại K.

Vậy góc HKB = 90 độ.

Nhưng ta đã chứng minh BE là tia phân giác của góc B, vậy góc HBE = góc EBK.

Vậy ta có: góc EBK + góc HKB = góc HBE + góc HKB = 60 + 90 = 150 độ.

Nhưng tổng các góc trong tam giác BKH là 180 độ, vậy góc EBK + góc HKB = 180 độ.

Từ đó suy ra góc EBK = 30 độ.

ΔAED vuông tại E

=>AE<AD

ΔCFD vuông tại F

=>CF<CD

AE<AD

CF<CD

Do đó: AE+CF<AD+CD=AC

Không có a và b thỏa mãn đề bài

Sửa đề; BA=BM

Xét ΔBAN và ΔBMN có

BA=BM

\(\widehat{ABN}=\widehat{MBN}\)

BN chung

Do đó: ΔBAN=ΔBMN

=>\(\widehat{BAN}=\widehat{BMN}\)

=>\(\widehat{BMN}=90^0\)

=>NM\(\perp\)BC

Xét ΔNAD vuông tại A và ΔNMC vuông tại M có

NA=NM(ΔBAN=ΔBMN)

\(\widehat{AND}=\widehat{MNC}\)(hai góc đối đỉnh)

Do đó: ΔNAD=ΔNMC

=>AD=MC

BC=BM+MC

mà BA=BM và MC=AD

nên BC=BA+AD

Đặt f(x)=0

=>(x-1)(x+2)=0

=>\(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Nghiệm của f(x) cũng là nghiệm của g(x)=0

=>\(\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(-2\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}1^3+a\cdot1^2+b\cdot1+2=0\\\left(-2\right)^3+a\left(-2\right)^2+b\left(-2\right)+2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a+b=-3\\4a-2b+2-8=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a+b=-3\\4a-2b=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a+b=-3\\2a-b=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3a=0\\a+b=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=0\\b=-3\end{matrix}\right.\)

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét ΔABC có AB<AC<BC

mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC

nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)

b: Xét ΔCDB có

CA,DK là các đường trung tuyến

CA cắt DK tại M

Do đó: M là trọng tâm của ΔCDB

=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot8=\dfrac{16}{3}\left(cm\right)\)

c: Gọi F là giao điểm của d với AC

Vì d là trung trực của AC

nên d\(\perp\)AC tại F và F là trung điểm của AC

Ta có:QF\(\perp\)AC

DA\(\perp\)AC

Do đó: QF//AD

Xét ΔCAD có

Flà trung điểm của CA

FQ//AD

Do đó: Q là trung điểm của CD

Xét ΔCDB có

M là trọng tâm của ΔCDB

Q là trung điểm của CD

Do đó: B,M,Q thẳng hàng