Tìm x,y biết: x/y=0,8và 2x+3y=46
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: H là trung điểm của BC
a: Xét ΔAHB và ΔAHC có
AB=AC
AH chung
HB=HC
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔAMH và ΔANH có
AM=AN
\(\widehat{MAH}=\widehat{NAH}\)
AH chung
Do đó: ΔAMH=ΔANH
=>HM=HN
c: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC

Bạn ơi, bạn bổ sung đề trước đi ạ. Đây mới là phần sau của đề thôi

a)Xét 2 tam giác ABH và ACH có:
AB=AC(do tam giác ABC cân tại A)
Góc ABC bằng góc ACB (do tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=>Tam giác ABH = tam giác ACH(cạnh - góc - cạnh)
b)Xét 2 tam giác HBA và HCM có:
Góc AHB bằng góc CHM(2 góc đối đỉnh)
HA=HM(giả thiết)
BH=HC(H là trung điểm BC)
=>Tam giác HBA bằng tam giác HCM(cạnh-góc-cạnh)
=>Góc ABH=góc MCH(2 góc tương ứng)
mà 2 góc này nằm ở vị trí so le trong của đường thẳng AB và MC nên MC//AB
c)Xét tam giác ACM có:
CH là đường trung tuyến(H là trung điểm AM)
AF là đường trung tuyến(F là trung điểm MC)
Mà AF cắt CH tại G(do AF cắt BC tại G;H thuộc BC;G thuộc CH)
=>G là trọng tâm của tam giác ACM
Ta có:
ME cũng là 1 đường trung tuyến của tam giác ACM (E là trung điểm AC)
=>G thuộc ME ( tính chất 3 đường trung tuyến)
=>M,G,E thẳng hàng
`#3107.101107`
`a)`
Vì `\triangle ABC` cân tại A
`\Rightarrow`\(\text{AB = AC; }\widehat{\text{ABC}}=\widehat{\text{ACB}}\)
Xét `\triangle ABH` và `\triangle ACH`:
`\text{AB = AC}`
\(\widehat{\text{ABC}}=\widehat{\text{ACB}}\)
\(\text{HB = HC (H là trung điểm BC)}\)
\(\Rightarrow\) `\triangle ABH = \triangle ACH (c - g - c)`
`b)`
Xét `\triangle AHB` và `\triangle MHC`:
\(\text{AH = HM}\)
\(\widehat{\text{AHB}}=\widehat{\text{MHC}}\left(\text{đối đỉnh}\right)\)
\(\text{HB = HC }\)
`\Rightarrow \triangle AHB = \triangle MHC (c-g-c)`
\(\Rightarrow\widehat{\text{ABH}}=\widehat{\text{MCH}}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí sole trong
\(\Rightarrow\text{ }\text{MC // AB (tính chất)}\)
`c)`
Vì E là trung điểm của AC; F là trung điểm của MC
\(\Rightarrow\text{EA = EC; FM = FC}\)
Ta có:
\(\left\{{}\begin{matrix}\text{EA = EC}\\\text{FM =FC}\\\text{HA = HM}\end{matrix}\right.\)
\(\Rightarrow\text{AF; ME và CH}\) lần lượt là các đường trung tuyến của `\triangle ACM`
Mà AF cắt HC tại G
\(\Rightarrow\) G là trọng tâm của `\triangle ACM`
\(\Rightarrow\) \(\text{G}\in\text{ME}\)
\(\Rightarrow\) `3` điểm M, G, E thẳng hàng (đpcm).
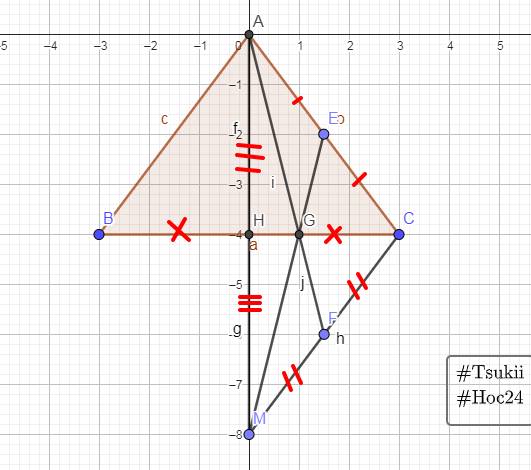

Trong tam giác ABC, áp dụng định lý về tổng 3 góc:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\Leftrightarrow120^0+2.\widehat{ABC}=180^0\) (do \(\widehat{ABC}=\widehat{ACB}\))
\(\Leftrightarrow\widehat{ABC}=30^0\)
Vậy góc tạo bởi mái nhà AB và vách tường BE là:
\(180^0-\left(\widehat{ABC}+\widehat{EBC}\right)=180^0-\left(30^0+90^0\right)=60^0\)

Gọi A là biến cố "Số xuất hiện trên thẻ được rút ra là số chia 4 dư 2"
=>A={2;6;10;14;18;22;26;30}
=>n(A)=8
\(n\left(\Omega\right)=30-1+1=30\)
\(P_A=\dfrac{8}{30}=\dfrac{4}{15}\)

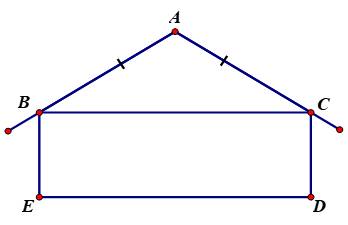
Bài 1
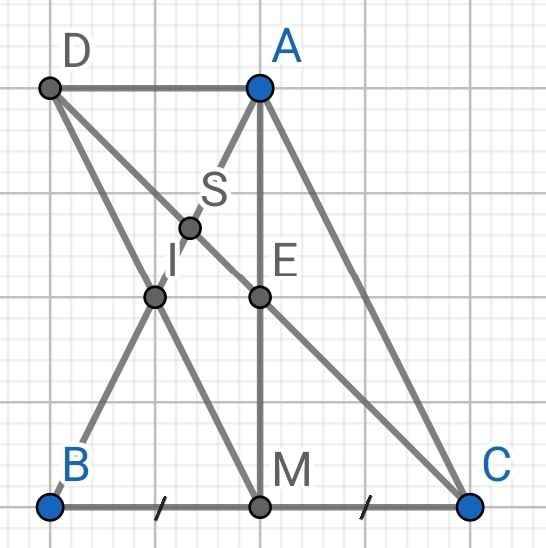
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét ∆AMB và ∆AMC có:
AB = AC (cmt)
BC = MC (cmt)
AM là cạnh chung
⇒ ∆AMB = ∆AMC (c-c-c)
b) Do AD // BC (gt)
⇒ AD // BM
⇒ ∠DAI = ∠MBI (so le trong)
Xét ∆AID và ∆BIM có:
∠DAI = ∠MBI (cmt)
AI = BI (do I là trung điểm của AB)
∠AID = ∠BIM (đối đỉnh)
⇒ ∆AID = ∆BIM (g-c-g)
⇒ AD = BM (hai cạnh tương ứng)
Mà BM = MC (cmt)
⇒ AD = MC
c) ∆AMB = ∆AMC (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
⇒ ∠AMC = ∠EMC = 90⁰
⇒ ∆MCE vuông tại M
Mà AD // BC (cmt)
⇒ AD ⊥ AM
⇒ ∠DAM = ∠DAE = 90⁰
⇒ ∆ADE vuông tại A
Do AD // BC (gt)
⇒ ∠ADE = ∠MCE (so le trong)
Xét hai tam giác vuông: ∆ADE và ∆MCE có:
AD = MC (cmt)
∠ADE = ∠MCE (cmt)
⇒ ∆ADE = ∆MCE (cạnh góc vuông - góc nhọn kề)
⇒ AE = ME (hai cạnh tương ứng)
⇒ E là trung điểm của AM
Do ∆AID = ∆BIM (cmt)
⇒ ID = IM (hai cạnh tương ứng)
⇒ I là trung điểm của MD
∆ADM có:
AI là đường trung tuyến (do I là trung điểm của MD)
DE là đường trung tuyến (do E là trung điểm của AM)
Mà AI và DE cắt nhau tại S
⇒ S là trọng tâm của ∆ADE
⇒ AS = 2SI
⇒ 3AS = 6SI
Lại có:
AI = BI (cmt)
⇒ AB = AI + BI = 3SI + 3SI = 6SI
⇒ AB = 3AS
Mà AB > BC (gt)
⇒ 3AS > BC
Hay BC < 3AS
Bài 3
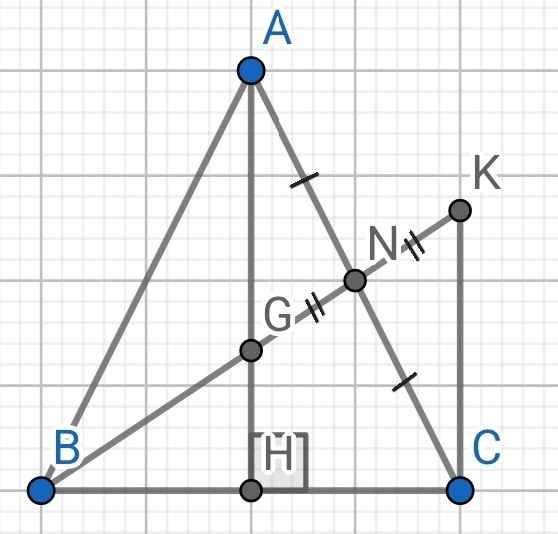
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AB = AC (cmt)
AH là cạnh chung
⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
b) ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung tuyến của ∆ABC
Lại có N là trung điểm của AC (gt)
⇒ BN là đường trung tuyến thứ hai của ∆ABC
Mà AH và BN cắt nhau tại G (gt)
⇒ G là trọng tâm của ∆ABC
Xét ∆ANG và ∆CNK có:
AN = CN (do N là trung điểm của AC)
∠ANG = ∠CNK (đối đỉnh)
NG = NK (gt)
⇒ ∆ANG = ∆CNK (c-g-c)
⇒ ∠AGN = ∠CKN (hai góc tương ứng)
Mà ∠AGN và ∠CKN là hai góc so le trong
⇒ AG // CK
c) Do G là trọng tâm của ∆ABC (cmt)
⇒ AG = 2GN
Lại có:
NG = NK (gt)
⇒ GK = 2GN
Mà BG = 2GN (cmt)
⇒ BG = GK
⇒ G là trung điểm của BK
x/y = 0,8 = 4/5
⇒ x/4 = y/5
⇒ 2x/8 = 3y/15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/8 = 3y/15 = (2x + 3y)/(8 + 15) = 46/23 = 2
x/4 = 2 ⇒ x = 2.4 = 8
y/5 = 2 ⇒ y = 2.5 = 10
Vậy x = 8; y = 10