Do x₀ là nghiệm của phương tình x²-m(m+4)x+m²+2m-1=0 nên tồn tại m để x₀² -(m+4)x₀+m²+2m-1=0

<=> m²+(2-x₀)m+x₀²-4x₀ -1=0 có nghiệm

<=> (2-x₀)² -4(x₀²-4x₀-1) >=0

<=> -3x₀²+12x₀+8 >=0

<=> \(\frac{6-2\sqrt{15}}{3}\le x_0\le\frac{6+2\sqrt{15}}{3}\)

Tự xử lý phần dấu "="

ez

Ta có : [ x ] \(\le\)x ;[ y ] \(\le\)y

\(\Rightarrow\)[ x ] + [ y ] \(\le\)x + y

Nên [ x ] + [ y ] là số nguyên không vượt quá x + y

mà [ x + y ] là số nguyên lớn nhất không vượt quá x + y

Do đó : [ x ] + [ y ] \(\le\)[ x + y ]

x=4

y=3

\(x^2-2\left(m+1\right)x+4m-4=0\left(a=1;b=-2\left(m+1\right);c=4m-4\right)\)

Ta có \(\Delta'=\left(-\left(m+1\right)\right)^2-1.\left(4m-4\right)\)

              \(=m^2+2m+1-4m+4\)

              \(=m^2-2m+5\)

              \(=\left(m-1\right)^2+4\)

Để phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow\left(m-1\right)^2+4>0\forall m\) (vì \(\left(m-1\right)^2\ge0\forall m\) ) (ĐPCM)

GMHCjgf,ghj,,g,gjmghfmjfg

Giải chi tiết:

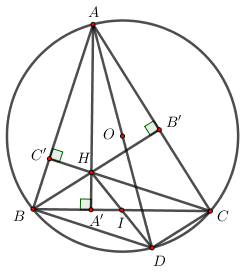
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.

Xét tứ giác AB’HC’ có ∠AB′H+∠AC′H=900+900=1800⇒∠AB′H+∠AC′H=900+900=1800⇒ Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).

b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.

Ta có ∠ABD=900∠ABD=900 (góc nội tiếp chắn nửa đường tròn) ⇒AB⊥BD⇒AB⊥BD.

Mà CH⊥AB(gt)⇒BD∥CHCH⊥AB(gt)⇒BD∥CH

Chứng minh tương tự ta có CD∥BHCD∥BH.

⇒⇒ Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)

Mà BC∩HD=I(gt)⇒IBC∩HD=I(gt)⇒I là trung điểm của BC.

c) Tính AHAA′+BHBB′+CHCC′AHAA′+BHBB′+CHCC′.

Ta có:

SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′

Chứng minh tương tự ta có: BHBB′=1−SHACSABC;CHCC′=1−SHABSABCBHBB′=1−SHACSABC;CHCC′=1−SHABSABC

⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2

Bài này giải theo cách lớp 9 thì thực sự bó tay. 
Đặt x = y - 2/3

\(x^3+2x^2-23x+8=0\) 

\(\left(y-\frac{2}{3}\right)^3+2\left(y-\frac{2}{3}\right)^2-23\left(y-\frac{2}{3}\right)+8=0\)

\(\Leftrightarrow y^3-2y^2+\frac{4}{3}y-\frac{8}{27}+2y^2-\frac{8}{3}y+\frac{8}{9}-23y+\frac{46}{3}+8=0\)

\(\Leftrightarrow y^3-\frac{73}{3}y+\frac{646}{27}=0\) (1)

Đặt \(a=\sqrt{-\frac{4}{3}.\frac{-73}{3}}=\frac{2\sqrt{73}}{3}\)

Đặt \(y=a.\cos t\)

 với \(0\le t\le\pi\)

Thay vào (1), ta có: 

\(a^3\cos^3t-\frac{73}{3}a\cos t=-\frac{646}{27}\)

\(\Leftrightarrow\frac{292}{9}.\frac{2\sqrt{73}}{3}\cos^3t-\frac{73}{3}.\frac{2\sqrt{73}}{3}\cos t=-\frac{646}{27}\)

\(\Leftrightarrow-\frac{73}{3}.\frac{2\sqrt{73}}{3}\left(-\frac{4}{3}\cos^3t+\cos t\right)=-\frac{646}{27}\)

\(\Leftrightarrow146\sqrt{73}\left(4\cos^3t-3\cos t\right)=646\)

\(\Leftrightarrow146\sqrt{73}.\cos\left(3t\right)=646\)

\(\cos\left(3t\right)=\frac{323\sqrt{73}}{5329}\)

\(t=\frac{\pm arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}+\frac{2k\pi}{3}\left(k\in Z\right)\)

Vì \(0\le t\le\pi\)

\(\Rightarrow t=\frac{arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}\) hoặc \(t=\frac{arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}+\frac{2\pi}{3}\)hoặc \(t=\frac{-arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}+\frac{2\pi}{3}\)

\(x=y+\frac{2}{3}=-\frac{73}{3}\cos t+\frac{2}{3}\)

Vậy nghiệm của pt là 

\(\left\{-\frac{73}{3}\cos\frac{arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}+\frac{2}{3};-\frac{73}{3}\cos\left(\frac{arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}+\frac{2\pi}{3}\right)+\frac{2}{3};-\frac{73}{3}\cos\left(\frac{-arccos\left(\frac{323\sqrt{73}}{5329}\right)}{3}+\frac{2\pi}{3}\right)+\frac{2}{3}\right\}\)

Các góc đều ở chế độ radian (Hàm arccos trong casio là cos^-1)

***P/S: giải theo lớp 9 thì chịu

Nhầm: Đổi \(-\frac{73}{3}\) thành \(\frac{2\sqrt{73}}{3}\)mới đúng