Cả nhà giúp em câu C với ạ. Em cảm ơn!
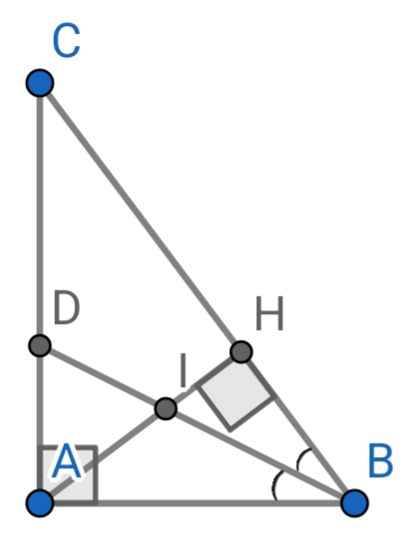
Bài 5 (2,5 điểm). Cho tam giác ABC vuông tại A có AH là đường cao.
a. Chứng minh rằng tam giác CBA đồng dạng CAH và AC2 = BH.CH .
b. Tia phân giác của góc AHC cắt AC tại K. Biết rằng độ dài các cạnh AH và CH lần lượt lả 6cm và 8cm. Tính độ dài BC và AK.
c. Lấy M là trung điểm của BC, N là trung điểm của AB. Qua B kẻ đường thẳng vuông góc với BC cắt đường thẳng MN tại D. Nối CD cắt AH tại I. Chứng minh I là trung điểm của AH.