abcdx4=dcba abcd=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để x + 495 và 195 - x đều chia hết cho x và x là số tự nhiên lớn nhất thì x = ƯCLN(495; 195)
Ta có:
495 = 3².5.11
195 = 3.5.13
⇒ x = ƯCLN(495; 195) = 3.5 = 15

Có 346 số tự nhiên có 4 chữ số chia hết cho 26. Chúc bạn học tốt!!!!!!

M=1x2+2x3+3x4+xxx+19x20
3M=1x2x3+2x3x3+3x4x3+xxx+19x20x3
3M=1x2x(3-0)+2x3x(4-1)+3x4x(5-2)+xxx+19x20x(21-18)
3M=(1x2x3-0x1x2)+(2x3x4-1x2x3)+(3x4x5-2x3x4)+xxx+(19x20x21-18x19x20)
3M=19x20x21-0x1x2
3M=7980-0
3M=7980
M=7980:3
M=2660
Vậy M=2660
Chúc bạn học tốt nha!!!!! ^^
\(A=1\cdot2+2\cdot3+...+19\cdot20\)
\(=1\left(1+1\right)+2\left(2+1\right)+...+19\left(19+1\right)\)
\(=\left(1^2+2^2+...+19^2\right)+\left(1+2+...+19\right)\)
\(=\dfrac{19\left(19+1\right)\left(2\cdot19+1\right)}{6}+\dfrac{19\cdot20}{2}\)
\(=2470+190=2660\)


Sau ngày 1 thì số trang còn lại chiếm:
\(1-50\%=\dfrac{1}{2}\)(quyển sách)
Sau ngày 2 thì số trang còn lại chiếm:
\(\dfrac{1}{2}\cdot\left(1-40\%\right)=\dfrac{1}{2}\cdot\dfrac{3}{5}=\dfrac{3}{10}\)(quyển sách)
3 trang cuối cùng chiếm:
\(\dfrac{3}{10}\left(1-80\%\right)=\dfrac{3}{10}\cdot\dfrac{1}{2}=\dfrac{3}{20}\)(quyển sách)
Quyển sách có \(3:\dfrac{3}{20}=20\left(trang\right)\)


Quãng đường xe máy đi được trong 1/2 giờ là:
40×1/2= 20 (km)
Hiệu vận tốc của ô tô và xe máy là:
55 – 40 = 15 (km/giờ)
Thời gian đi để ô tô đuổi kịp xe máy là:
20 : 15 = 4/3 (giờ) = 1 giờ 20 phút
Đáp số: 1 giờ 20 phút
Chúc bạn học tốt nha!!!!!! ^^

\(E=\left(2-x\right)\left(1+2x\right)+\left(1+x\right)-\left(x^4+x^3-5x^2-5\right)\)
\(=2+4x-x-2x^2+1+x-x^4-x^3+5x^2+5\)
\(=-x^4-x^3+\left(-2x^2+5x^2\right)+\left(4x-x+x\right)+\left(2+1+5\right)\)
\(=-x^4-x^3+3x+4x+8\)
--------
\(G=\left(x^2-7\right)\left(x+2\right)-\left(2x-1\right)\left(x-14\right)+x\left(x^2-2x-22\right)+35\)
\(=x^3+2x^2-7x-14-2x^2+28x+x-14+x^2-2x^2-22x+35\)
\(=x^3+\left(2x^2-2x^2+x^2-2x^2\right)+\left(-7x+28x+x-22x\right)+\left(-14-14+35\right)\)
\(=x^3-x^2+7\)
--------
\(D=\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(x+5\right)-6\left(3x-2\right)\)
\(=6x^2+21x-2x-7-x^2-5x-x-5-18x+12\)
\(=\left(6x^2-x^2\right)+\left(21x-2x-5x-x-18x\right)+\left(-7-5+12\right)\)
\(=5x^2-5x\)
\(E=\left(2-x\right)\left(1+2x\right)+\left(1+x\right)-\left(x^4+x^3-5x^2-5\right)\)
\(=2+4x-x-2x^2+1+x-x^4-x^3+5x^2+5\)
\(=-x^4-x^3+3x^2+4x+8\)
\(G=\left(x^2-7\right)\left(x+2\right)-\left(2x-1\right)\left(x-14\right)+x\left(x^2-2x-22\right)+35\)
\(=x^3+2x^2-7x-14-\left(2x^2-28x-x+14\right)+x^3-2x^2-22x+35\)
\(=2x^3-29x+21-2x^2+29x-14\)
\(=2x^3-2x^2+7\)
\(D=\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(x+5\right)-6\left(3x-2\right)\)
\(=6x^2+21x-2x-7-\left(x^2+6x+5\right)-18x+12\)
\(=6x^2+x+12-x^2-6x-5=5x^2-5x+7\)
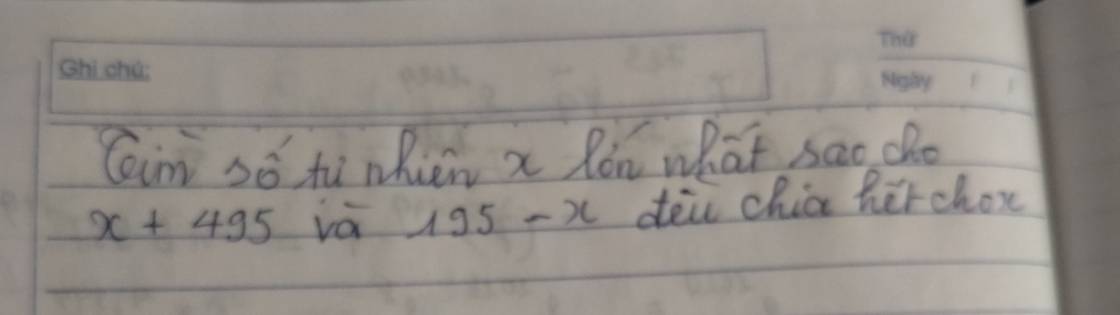
Để giải bài toán này, ta sẽ giải phương trình: ABCD x 4 = DCBA Ta biểu diễn số ABCD dưới dạng 1000A + 100B + 10C + D và số DCBA dưới dạng 1000D + 100C + 10B + A. Vậy phương trình trở thành: 1000A + 100B + 10C + D = 1000D + 100C + 10B + A Chuyển các thành phần về cùng một phía ta được: 999A - 90B - 90C + 999D = 0 999(A - D) - 90(B - C) = 0 Vì A, B, C, D là các chữ số từ 0 đến 9 nên ta có thể thử từng trường hợp để tìm ra kết quả. Dễ dàng thấy rằng A = 2, B = 1, C = 7, D = 8 thỏa mãn phương trình trên. Vậy số ABCD = 2178.