20,23 : 0,125 + 60,69 + 89 x 20,23
Help me , cần gấp !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1 tháng 4
\(7,75\times x+2,25\times x=50\)
=>\(x\times\left(7,75+2,25\right)=50\)
=>\(10\times x=50\)
=>x=5
1 tháng 4
a: Số phần đoạn dây chú Tuấn đã dùng hết:
\(\dfrac{1}{9}+\dfrac{1}{3}=\dfrac{4}{9}\)(đoạn dây)
b: Chú Tuấn còn lại là \(1-\dfrac{4}{9}=\dfrac{5}{9}\)(đoạn dây)
KV
1 tháng 4
a) 7/12 + 5/24 + 5/12 + 19/24
= (7/12 + 5/12) + (5/24 + 19/24)
= 1 + 1
= 2
b) 5/18 + 4/15 + 7/18 + 1/15
= (5/18 + 7/18) + (4/15 + 1/15)
= 2/3 + 1/3
= 1
c) 1/5 + 5/9 + 4/5 + 1/9
= (1/5 + 4/5) + (5/9 + 1/9)
= 1 + 1/3
= 4/3
d) 1/3 + 1/6 + 4/3 + 2/6 + 2/3 + 5/6
= (1/3 + 4/3 + 2/3) + (1/6 + 1/6 + 5/6)
= 7/3 + 7/6
= 7/2
DT
Dang Tung
CTVHS
1 tháng 4
a) \(\dfrac{7}{12}+\dfrac{5}{24}+\dfrac{5}{12}+\dfrac{19}{24}\\ =\left(\dfrac{7}{12}+\dfrac{5}{12}\right)+\left(\dfrac{5}{24}+\dfrac{19}{24}\right)\\ =\dfrac{7+5}{12}+\dfrac{5+19}{24}\\ =\dfrac{12}{12}+\dfrac{24}{24}\\ =1+1=2\)
b) \(\dfrac{5}{18}+\dfrac{4}{15}+\dfrac{7}{18}+\dfrac{1}{15}\\ =\left(\dfrac{5}{18}+\dfrac{7}{18}\right)+\left(\dfrac{4}{15}+\dfrac{1}{15}\right)\\ =\dfrac{5+7}{18}+\dfrac{4+1}{15}\\ =\dfrac{12}{18}+\dfrac{5}{15}\\ =\dfrac{1}{3}+\dfrac{1}{3}=\dfrac{1+1}{3}=\dfrac{2}{3}\)
KV
1 tháng 4
2 giờ 30 phút = 2,5 giờ
Quãng đường AB dài:
48 × 2,5 = 120 (km)
Nếu người đó đi ô tô với vận tốc 60 km/giờ thì mất khoảng thời gian là:
120 : 60 = 2 (giờ)
KV
1 tháng 4
a) 40 phút = 2/3 giờ
1 giờ 30 phút = 1,5 giờ
Vận tốc của Nam:
24 : 2/3 = 36 (km/giờ)
Quãng đường từ nhà Nam lên quận dài:
36 × 1,5 = 54 (km)
b) Muốn đến quận lúc 8 giờ 15 phút thì Nam phải khởi hành từ nhà lúc:
8 gờ 15 phút - 15 phút - 1 giờ 30 phút = 6 giờ 30 phút
1 tháng 4
\(A=\dfrac{5\cdot4^6\cdot9^4-3^9\cdot\left(-8\right)^4}{4\cdot2^{13}\cdot3^8+2\cdot8^4\cdot\left(-27\right)^3}\)
\(=\dfrac{5\cdot2^{12}\cdot3^8-3^9\cdot2^{12}}{2^{15}\cdot3^8-2^{13}\cdot3^9}\)
\(=\dfrac{2^{12}\cdot3^8\left(5-3\right)}{2^{13}\cdot3^8\left(2^2-3\right)}\)
\(=\dfrac{2^{13}}{2^{13}}=1\)
KV
1 tháng 4
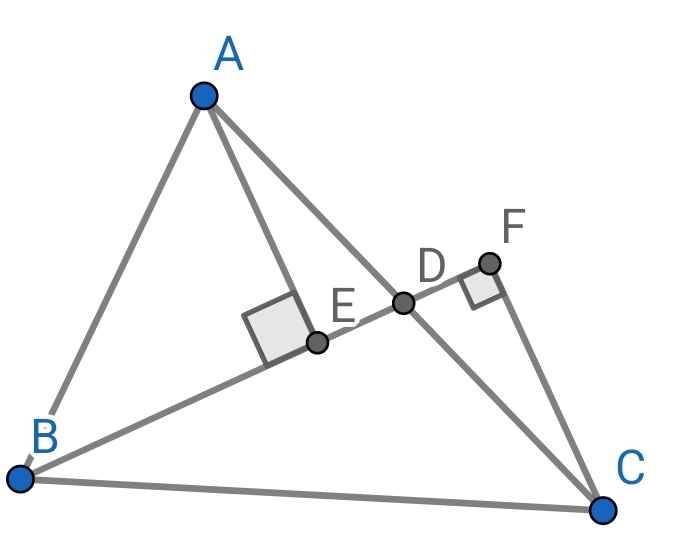
a) ∆ADE vuông tại E
⇒ AD là cạnh huyền nên là cạnh lớn nhất
⇒ AE < AD (1)
∆CDF vuông tại F
⇒ CD là cạnh huyền nên là cạnh lớn nhất
⇒ CF < CD (2)
Từ (1) và (2) ⇒ AE + CF < AD + CD
⇒ AE + CF < AC
b) Xét hai tam giác vuông: ∆ADE và ∆CDF có:
AD = CD (do D là trung điểm của AC)
∠ADE = ∠CDF (đối đỉnh)
⇒ ∆ADE = ∆CDF (cạnh huyền - góc nhọn)
⇒ AE = CF (hai cạnh tương ứng)
\(20,23:0,125+60,69+89\times20,23\)
\(=20,23\times8+20,23\times3+20,23\times89\)
\(=20,23\left(8+3+89\right)=20,23\times100=2023\)