Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất
ĐKXĐ: x ≥ 0
⇒ x + √x + 1 ≥ 1
⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0
Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0
Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất
ĐKXĐ: x ≥ 0
⇒ x + √x + 1 ≥ 1
⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0
Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0
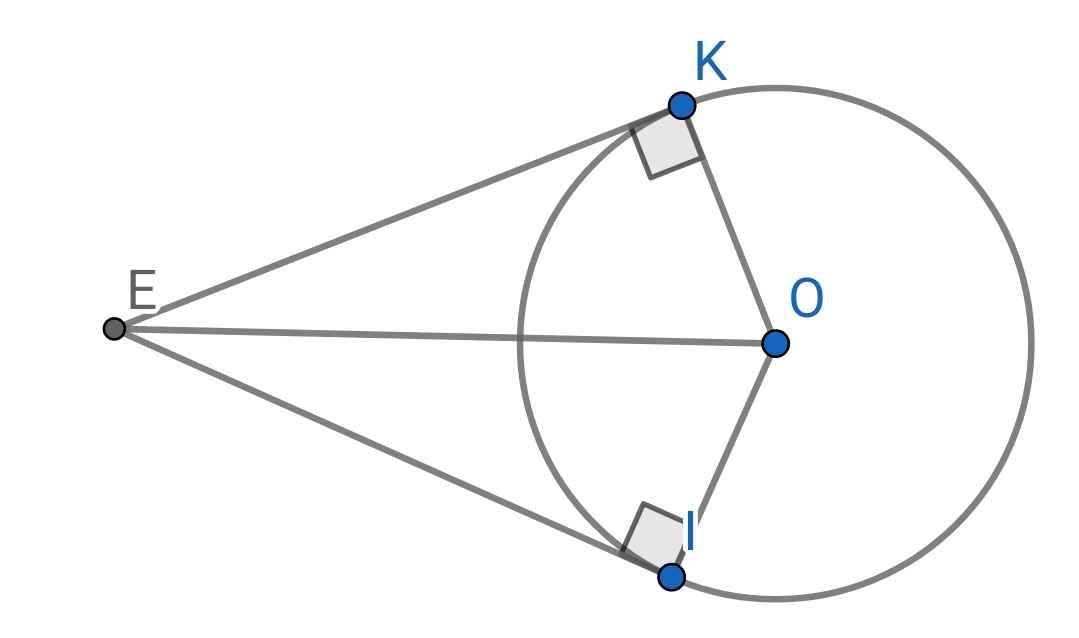Do EI là tiếp tuyến của (O) tại I
⇒ EI OI
⇒ ∆OEI vuông tại I
⇒ O, E, I cùng thuộc đường tròn đường kính OE (1)
Do EK là tiếp tuyến của (O) tại K
⇒ EK OK
⇒ ∆OEK vuông tại K
⇒ O, E, K cùng thuộc đường tròn đường kính OE (2)
Từ (1) và (2) suy ra E, I, O, K cùng thuộc đường tròn đường kính OE
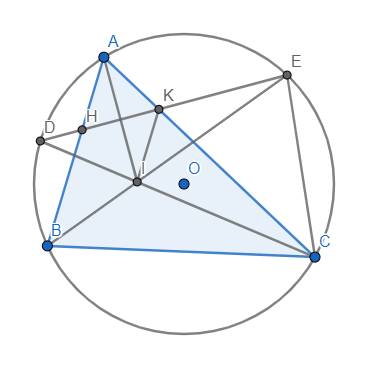
a) Ta có \(\widehat{AHK}=\dfrac{sđ\stackrel\frown{AE}+sđ\stackrel\frown{BD}}{2}\)
và \(\widehat{AKH}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\)
Mặt khác, do D, E lần lượt là điểm chính giữa của cung AB, AC nên \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD};sđ\stackrel\frown{AE}=sđ\stackrel\frown{CE}\). Từ đó \(\Rightarrow\widehat{AHK}=\widehat{AKH}\) hay tam giác AHK cân tại A (đpcm).
b) Hiển nhiên I là tâm đường tròn nội tiếp tam giác ABC \(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\) (hay chính là \(\widehat{HAK}\)). Mà theo câu a), tam giác AHK cân tại A nên AI đồng thời là đường cao của tam giác AHK \(\Rightarrow AI\perp HK\) hay \(AI\perp DE\) (đpcm)
c) Ta có \(\widehat{CIE}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{BD}}{2}\)
\(=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\) \(=\widehat{CKE}\) nên tứ giác CEKI nội tiếp
\(\Rightarrow\widehat{HKI}=\widehat{DCE}\) \(=\dfrac{sđ\stackrel\frown{DE}}{2}\)
\(=\dfrac{sđ\stackrel\frown{DA}+sđ\stackrel\frown{AE}}{2}\) \(=\dfrac{sđ\stackrel\frown{BD}+sđ\stackrel\frown{AE}}{2}\) \(=\widehat{AHK}\)
Từ đó dễ dàng suy ra KI//AH hay KI//AB (đpcm)
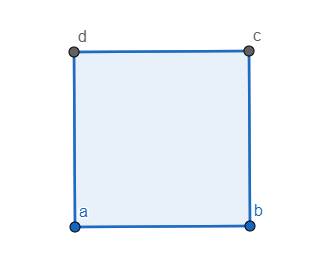
Xét 1 mặt bất kì của khối lập phương như hình vẽ và gọi 4 số ở đỉnh là a, b, c, d. Khi đó do \(a+b+c,b+c+d,c+d+a,d+a+b\ge10\) nên \(3\left(a+b+c+d\right)\ge40\) \(\Rightarrow a+b+c+d\ge14\)
Làm tương tự cho 4 mặt còn lại, ta đều được tổng của 4 số trên mỗi mặt đều không nhỏ hơn 14.
Nhưng trong một mặt, sẽ có mặt có chứa đỉnh mang số 8. Khi đó 3 đỉnh còn lại bắt buộc là 1, 2, 3, mà \(1+2+3< 10\), vô lí. Lập luận tương tự cho trường hợp GTNN là 15, 16, 17. Nếu GTNN là 18, ta chỉ ra 1 trường hợp dấu "=" xảy ra:
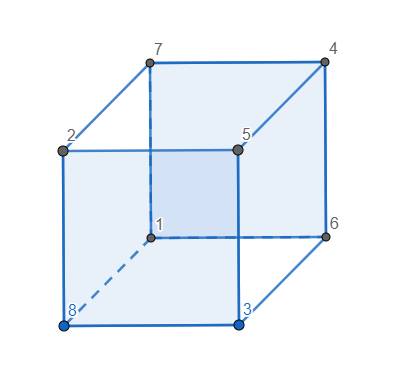
Vậy GTNN của 4 số trong cùng 1 mặt là 18.
Xét 2 đường thẳng: \(y=\left(m^2+2\right)x+m\left(d\right)\)
\(y=6x+2\left(d'\right)\)
Để \(\left(d\right)//\left(d'\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2+2=6\\m\ne2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\m\ne2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne2\end{matrix}\right.\)
\(\Leftrightarrow m=-2\)
Vậy.......
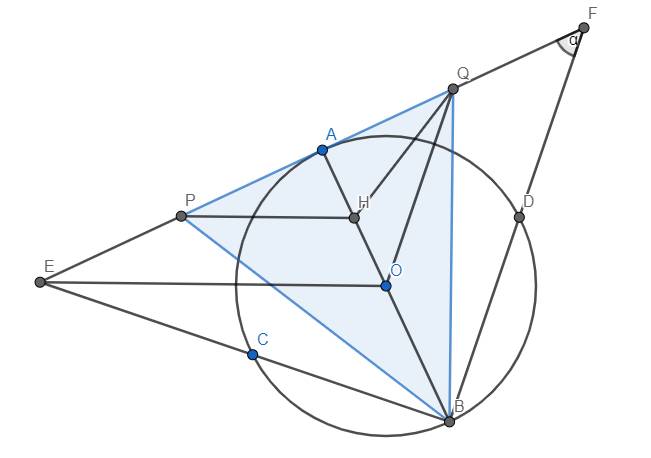
a) Định nghĩa lại H là trung điểm OA. Ta thấy OQ là đường trung bình của tam giác ABF nên OQ//BF. Hơn nữa \(BF\perp BE\) nên \(OQ\perp BE\). Lại có \(BA\perp QE\) nên O là trực tâm của tam giác BEQ \(\Rightarrow OE\perp BQ\)
Mặt khác, PH là đường trung bình của tam giác AOE nên PH//OA. Do đó, \(PH\perp BQ\). Lại thấy rằng \(BH\perp PQ\) nên H là trực tâm tam giác BPQ (đpcm)
b) Ta có \(P=\sin^6\alpha+\cos^6\alpha\)
\(=\left(\sin^2\alpha\right)^3+\left(\cos^2\alpha\right)^3\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^4\alpha+\cos^4\alpha-\sin^2\alpha\cos^2\alpha\right)\)
\(=1.\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-3\sin^2\alpha\cos^2\alpha\right]\)
\(=1-3\sin^2\alpha\cos^2\alpha\)
\(\le1-3.\dfrac{\left(\sin^2\alpha+\cos^2\alpha\right)^2}{4}\)
\(=\dfrac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\sin\alpha=\cos\alpha\) \(\Leftrightarrow\alpha=45^o\) hay 2 dây AB, CD vuông góc với nhau.
Vậy \(min_P=\dfrac{1}{4}\)
c) Ta có \(\left\{{}\begin{matrix}EC.EB=EA^2\\FD.FB=FA^2\end{matrix}\right.\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow EC.EB.FD.FB=\left(EA.FA\right)^2\)
\(\Rightarrow EC.FD.\left(EB.DB\right)=AB^4\)
\(\Rightarrow EC.FD.\left(EF.AB\right)=AB^4\)
\(\Rightarrow EC.FD.EF=AB^3=CD^3\) (đpcm)
Ta có \(EC.DF=AC.AD=BC.BD\)
\(\Rightarrow\dfrac{EC}{DF}=\dfrac{BC.BD}{DF^2}\)
\(=\dfrac{BC}{DF}.\dfrac{BD}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AC}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AE}{AF}\)
\(=\left(\dfrac{BE}{BF}\right)^3\)
Ta có đpcm.
Bài khá căng đấy
Lời giải:
Để $n^4+n^3+1$ là scp $\Leftrightarrow A=4n^4+4n^3+4$ cũng phải là scp
Xét $A-(2n^2+n+1)^2=4n^4+4n^3+4-(2n^2+n+1)^2=-5n^2-2n+3\leq -5-2n+3=-2-2n<0$ với mọi $n\geq 1$
$\Rightarrow A< (2n^2+n+1)^2(1)$
Xét $A-(2n^2+n-1)^2=4n^4+4n^3+4-(2n^2+n-1)^2=3n^2+2n+3>0$ với mọi $n\geq 1$
$\Rightarrow A> (2n^2+n-1)^2(2)$
Từ $(1); (2)\Rightarrow (2n^2+n-1)^2< A< (2n^2+n+1)^2$
$\Rightarrow A=(2n^2+n)^2$
$\Rightarrow (4n^4+4n^3+4)=(2n^2+n)^2$
$\Leftrightarrow 4-n^2=0$
$\Rightarrow n=2$
Lời giải:
$xy+yz+xz=1$
$\Rightarrow x^2+1=x^2+xy+yz+xz=(x+y)(x+z)$
Tương tự: $y^2+1=(y+z)(y+x); z^2+1=(z+x)(z+y)$
Khi đó:
\(\sum \sqrt{\frac{(x^2+1)(y^2+1)}{z^2+1}}=\sum \sqrt{\frac{(x+y)(x+z)(y+x)(y+z)}{(z+x)(z+y)}}=\sum \sqrt{(x+y)^2}\)
$=\sum (x+y)=2(x+y+z)$
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\))
Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)
Nên \(\widehat{HAC}\approx53,13^o\)
Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm
\(\Rightarrow IB=IC=20cm\)
Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)
Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)
Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)
\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)
Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)
Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)
\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)