Cho các số thực dương thỏa mãn:\(\frac{1}{a}\)+\(\frac{1}{2b}\)+\(\frac{1}{3c}\)=0 .Tính giá trị biểu thức Q=\(\frac{bc}{a^2}\)+\(\frac{ac}{8b^2}\)+\(\frac{ab}{27c^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(xy^2+\left(2x-27\right)y+x=0\)
Xét phương trình theo ẩn y. Để phương trình có nghiệm thì
\(\Delta_y=\left(2x-27\right)^2-4x.x\ge0\)
\(\Rightarrow1\le x\le6\)
Thế lần lược tực 1 tới 6 vô ta chỉ nhận \(\left(x;y\right)=\left(6;2\right)\)

Với x > 0 , áp dụng bđt AM-GM ta có :
\(\frac{x}{\left(x+1\right)^2}+\frac{\left(x+1\right)^2}{x}\ge2\sqrt{\frac{x}{\left(x+1\right)^2}\cdot\frac{\left(x+1\right)^2}{x}}=2\)
=> \(A=\frac{x}{\left(x+1\right)^2}+\frac{\left(x+1\right)^2}{x}-2\ge2-2=0\)
Đẳng thức xảy ra <=> \(\frac{x}{\left(x+1\right)^2}=\frac{\left(x+1\right)^2}{x}\)
=> ( x + 1 )4 - x2 = 0
<=> [ ( x + 1 )2 - x ][ ( x + 1 )2 + x ] = 0
<=> ( x2 + x + 1 )( x2 + 3x + 1 ) = 0
<=> \(\orbr{\begin{cases}x^2+x+1=0\\x^2+3x+1=0\end{cases}}\)
+) x2 + x + 1 = 0
Δ = b2 - 4ac = 1 - 4 = -3
Δ < 0 nên pt vô nghiệm
+) x2 + 3x + 1 = 0
Δ = b2 - 4ac = 9 - 4 = 5
Δ > 0, áp dụng công thức nghiệm thu được \(\hept{\begin{cases}x_1=\frac{-3+\sqrt{5}}{2}\\x_2=\frac{-3-\sqrt{5}}{2}\end{cases}}\left(ktm\right)\)
Vậy ...

Trả lời:
( x - 4 )2 + ( x + 5 )2 = 0
Vì \(\left(x-4\right)^2\ge0\forall x\); \(\left(x+5\right)^2\ge0\forall x\)
=> ( x - 4 )2 = 0 và ( x + 5 )2 = 0
<=> x - 4 = 0 và x + 5 = 0
<=> x = 4 và x = -5
Vậy x = 4 và x = -5
( x - 4 )2 + ( x + 5 )2 = 0
<=> x2 - 8x + 16 + x2 + 10x + 25 = 0
<=> 2x2 + 2x + 41 = 0
Δ = b2 - 4ac = 22 - 4.2.41 = 4 - 328 = -324
Δ < 0 nên pt vô nghiệm

Dùng phương pháp hệ số bất định , rồi đồng nhất hệ số nha
\(x^4-8x+63=x^4+16x^2-16x^2-8x+64-1\)
\(=(x^4+16x^2+64)-\left(16x^2+8x+1\right)\)
\(=\left(x^2+8\right)^2-\left(4x+1\right)^2=\left(x^2+8+4x+1\right)\left(x^2+8-4x-1\right)\)
\(=\left(x^2+4x+9\right)\left(x^2-4x+7\right)\)

c) Đặt AB = a (không đổi)
Xét \(\Delta DAF\)và \(\Delta BAE\)có:
\(\widehat{ADF}=\widehat{ABE}\left(=90^0\right)\)
\(AD=AB\)(vì ABCD là hình vuông)
\(\widehat{DAF}=\widehat{BAE}\)(cùng phụ với \(\widehat{DAE}\))
\(\Rightarrow\Delta DAF=\Delta BAE\left(g.c.g\right)\left(1\right)\)
\(\Rightarrow AF=AE\)(2 cạnh tương ứng) (2) ;
Xét \(\Delta AFE\)vuông tại A (vì \(Ax\perp AE\)) có : (2)
\(\Rightarrow\Delta AFE\)vuông cân tại A
Có trung tuyến AI ứng với cạnh huyền BC
\(\Rightarrow\)AI đồng thời là đường cao ứng với BC
Xét \(\Delta KEF\)có: AI vừa là trung tuyến, đồng thời là đường cao ứng với cạnh BC
\(\Rightarrow\Delta KEF\)cân tại K.
\(\Rightarrow KE=KF\)(định nghĩa)
Từ (2) \(\Rightarrow BE=DF\)(2 cạnh tương ứng)
Ta có:
\(P_{\Delta CKE}=CK+CE+EK\)
\(P_{\Delta CKE}=CK+CE+FK\)(vì \(FK=EK\))
\(P_{\Delta CKE}=CK+CE+FD+DK\)
\(P_{\Delta CKE}=\left(CK+DK\right)+\left(CE+FD\right)\)
\(P_{\Delta CKE}=CD+\left(CE+BE\right)\)(vì \(FD=BE\))
\(P_{\Delta CKE}=CD+BC=AB+AB=2AB=2a\)(không đổi)
Do đó chu vi \(\Delta CKE\)luôn không đổi (điều phải chứng minh)
Vậy chu vi \(\Delta CKE\)luôn không đổi.
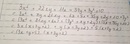
Đặt \(a=x;2b=y;3c=z\)
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
\(\Leftrightarrow xy+yz+zx=0\)
\(\Rightarrow Q=\frac{\frac{y}{2}.\frac{z}{3}}{x^2}+\frac{x.\frac{c}{3}}{2y^2}+\frac{x.\frac{y}{2}}{3z^2}\)
\(=\frac{x^3y^3+y^3z^3+z^3x^3}{6x^2y^2z^2}\)
\(=\frac{x^3y^3+y^3z^3+z^3x^3-3x^2y^2z^2+3x^2y^2z^2}{6x^2y^2z^2}\)
\(=\frac{\left(xy+yz+zx\right)\left(x^2y^2+y^2z^2+z^2x^2-x^2yz-y^2zx+z^2xy\right)+3x^2y^2z^2}{6x^2y^2z^2}\)
\(=\frac{3x^2y^2z^2}{6x^2y^2z^2}=\frac{1}{2}\)