28-23*{50+[65-(109)]}
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đây không phải là toán lớp 1, em cần đăng câu hỏi đúng khối lớp, cảm ơn em.
Phương trình tương đương: \(1\cdot2\cdot3\cdot...\cdot x\cdot76\cdot77\cdot...\cdot100=1\cdot2\cdot3\cdot...\cdot100\)
và tìm được \(x=75\)

Bài 1
5 + 7 = 12
Bài 2:
Không phải là toán lớp 1

3x + 2y = 4
2y = 4 - 3x
⇒5x - 2y = 5x - (4- 3x)= 5x - 4 + 3x = (5x + 3x) - 4 = 8x -4 = 16
8x= 16 + 4
8x = 20
x = 20 : 8
x = \(\dfrac{5}{2}\)
thay x = \(\dfrac{5}{2}\) vào biểu thức 3x + 2y = 4 ta có
3.\(\dfrac{5}{2}\) + 2y = 4
\(\dfrac{15}{2}\) + 2y = 4
2y = 4 - \(\dfrac{15}{2}\)
2y = \(\dfrac{8}{2}\) - \(\dfrac{15}{2}\)
2y = \(-\dfrac{7}{2}\)
y = \(-\dfrac{7}{2}\) : \(2\)
y = \(-\dfrac{7}{4}\)
Vậy x = \(\dfrac{5}{2}\); y =\(-\dfrac{7}{4}\)


Đây là cách trình bày bằng lời giải (Cách trình bày bằng phép tính mình đã làm ở câu có dạng tương tự cho bạn rồi nhé, đều kèm của công thức rồi nhé)
Biểu thức A có số số hạng là:
`(1996 - 1) : 1 + 1 = 1996` (số hạng)
Giá trị của A là:
`(1 + 1996)` x `1996 : 2`
`= 1993006 `
Vậy `A = 1993006 `
Số lượng số hạng:
(1996 - 1) : 1 + 1 = 1996
Tổng của dãy số:
A = (1996 + 1) x 1996 : 2 = 1993006
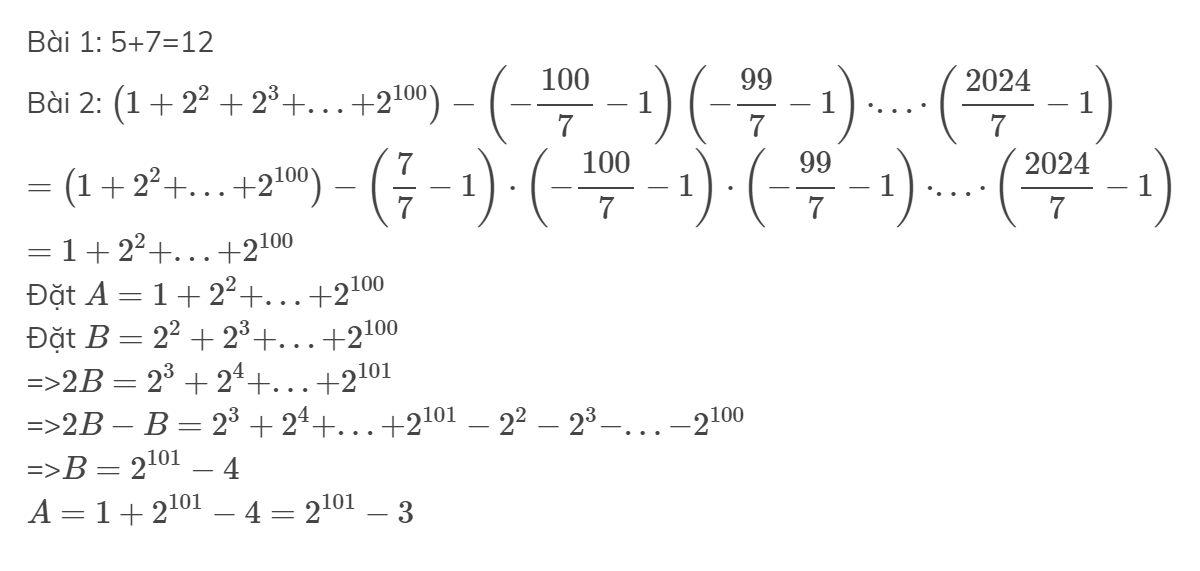
28 - 23 x {50 + [65 - (109)]}
= 28 - 23 x {50 + [65 - 109]}
= 28 - 23 x {50 - 44}
= 28 - 23 x 6
= 28 - 138
= - 110
Đây không phải là toán lớp 10, em cần chú ý khi đăng câu hỏi em nhé!