Để chứng minh rằng \( \frac{1}{x} + \frac{1}{y} = 1 \), ta bắt đầu từ phương trình \( \frac{x}{y} + \frac{y}{x} = 3 \):
\( \frac{x}{y} + \frac{y}{x} = 3 \)
Nhân cả hai vế với \(xy\), ta có:
\(x^2 + y^2 = 3xy\)
Tiếp theo, ta nhân cả hai vế của phương trình thứ hai \( \frac{x^2}{y} + \frac{y^2}{x} = 10 \) với \(x + y\), ta có:
\(x^3 + y^3 + xy(x + y) = 10(x + y)\)
Vì \(x \neq 0\) và \(y \neq 0\), nên \(x + y \neq 0\). Ta có thể chia cả hai vế cho \(x + y\):
Xin lỗi về sự gián đoạn. Bây giờ chúng ta có hai phương trình:
1. \(x^2 + y^2 = 3xy\)
2. \(x^3 + y^3 + xy = 10\)
Ta có thể thay \(x^2 + y^2\) từ phương trình thứ nhất vào phương trình thứ hai:
\(x^3 + y^3 + 3xy = 10\)
Lưu ý rằng \(x\) và \(y\) khác 0. Ta có thể chia cả hai vế cho \(xy\) mà không làm mất tính chất của phương trình:
\(\frac{x^3}{xy} + \frac{y^3}{xy} + 3 = \frac{10}{xy}\)
\(\frac{x^2}{y} + \frac{y^2}{x} + 3 = \frac{10}{xy}\)
Thay \(x^2/y + y^2/x\) từ phương trình ban đầu vào, ta có:
\(3 + 3 = \frac{10}{xy}\)
\(6 = \frac{10}{xy}\)
Từ đó, ta có \(xy = \frac{10}{6} = \frac{5}{3}\).
Cuối cùng, ta có thể thay \(xy\) trở lại vào phương trình ban đầu:
\(x^2 + y^2 = 3 \cdot \frac{5}{3}\)
\(x^2 + y^2 = 5\)
Bây giờ, ta có thể sử dụng bổ đề Pythagoras: \(x^2 + y^2 = (x + y)^2 - 2xy\).
Ta biết rằng \(x^2 + y^2 = 5\) và \(xy = \frac{5}{3}\). Vậy nên:
\(5 = (x + y)^2 - 2 \cdot \frac{5}{3}\)
\(5 = (x + y)^2 - \frac{10}{3}\)
\(15 = 3(x + y)^2 - 10\)
\(25 = 3(x + y)^2\)
\(x + y = \pm \sqrt{\frac{25}{3}} = \pm \frac{5}{\sqrt{3}} = \pm \frac{5\sqrt{3}}{3}\)
Do \(x\) và \(y\) không thể bằng 0, nên \(x + y\) không thể bằng 0. Vậy nên:
\(x + y = \frac{5\sqrt{3}}{3}\)
Và từ đó:
\(\frac{1}{x} + \frac{1}{y} = \frac{x + y}{xy} = \frac{\frac{5\sqrt{3}}{3}}{\frac{5}{3}} = 1\)
Vậy nên, chúng ta đã chứng minh được \( \frac{1}{x} + \frac{1}{y} = 1 \).
\(x^3 + y^3 +

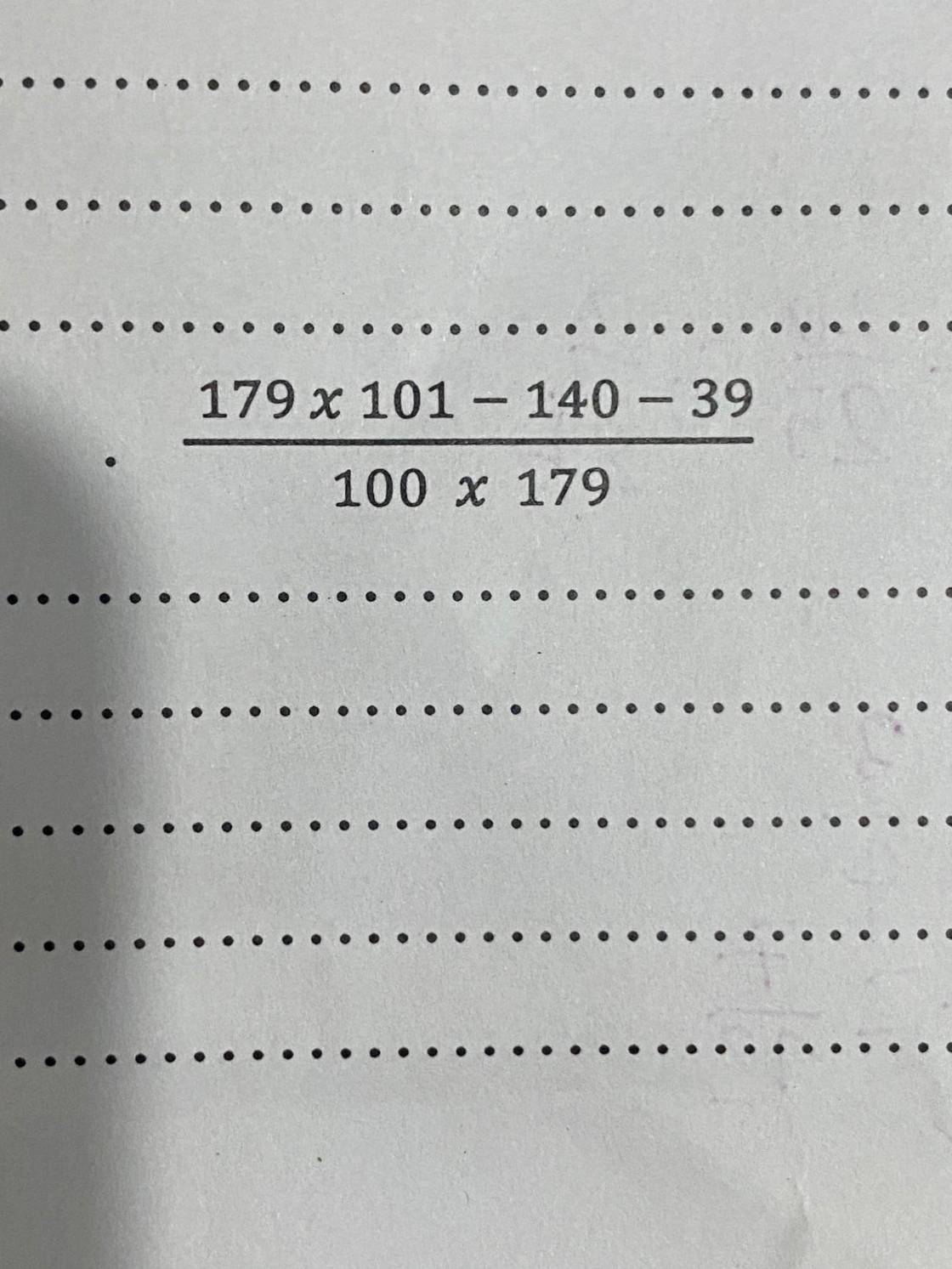




???????????? V ĐĂNG LÊN LMJ
Đây là câu trl r bn ưi