Chứng minh rằng: Với mọi \(n\) là số nguyên chẵn thì \(\dfrac{n}{12}+\dfrac{n^2}{8}+\dfrac{n^3}{24}\) là số nguyên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhận thấy \(a\) phải là số nguyên tố lẻ.
Xét \(a=3\). Khi đó \(3^2+8=17\) là snt. Lúc này \(3^2+2=11\) cũng là snt (thỏa mãn).
Xét \(a>3\). Khi đó vì \(a\) là snt nên \(a⋮̸3\) \(\Rightarrow a^2\equiv1\left[3\right]\) \(\Rightarrow a^2+8⋮3\), không thỏa mãn.
Do đó để \(a\) và \(a^2+8\) là snt thì \(a=3\)
Vậy ta có đpcm.
Nếu \(a=2\Rightarrow a^2+8=12\) là hợp số (loại)
Nếu \(a=3\Rightarrow a^2+8=17\) cũng là SNT, khi đó \(a^2+2=11\) là SNT (thỏa mãn)
Nếu \(a>3\Rightarrow a\) ko chia hết cho 3 \(\Rightarrow a^2\) chia 3 luôn dư 1
\(\Rightarrow a^2+8\) chia hết cho 3 \(\Rightarrow\) là hợp số (loại)
Vậy ...

\(x^2+3y^2+4x+10y-14=0\)
\(\Leftrightarrow\left(x+2\right)^2+3y^2+10y=18\) (1)
\(\Rightarrow3y^2+10y\le18\)
\(\Rightarrow2y^2+8y\le3y^2+10y\le18\)
\(\Rightarrow2y^2+8y+8\le26\)
\(\Rightarrow\left(y+2\right)^2\le13\)
Mà \(y\) nguyên và \(y\ge0\) \(\Rightarrow y=\left\{0;1\right\}\)
- Với \(y=0\) thay vào (1) \(\Rightarrow\left(x+2\right)^2=18\) ko tồn tại x nguyên thỏa mãn
- Với \(y=1\) thay vào (1) \(\Rightarrow\left(x+2\right)^2+13=18\Rightarrow\left(x+2\right)^2=5\) không tồn tại x nguyên thỏa mãn
Vậy ko tồn tại các số nguyên không âm x; y thỏa mãn

\(x^2-2\left(3m-1\right)x+12m-8=0\)
Để pt có 2 nghiệm phân biệt
Thì : \(\Delta'=\left[-\left(3m-1\right)\right]^2-1.\left(12m-8\right)>0\)
\(=>9m^2-6m+1-12m+8>0\\ =>9m^2-18m+9>0\\ =>m^2-2m+1>0\\ =>\left(m-1\right)^2>0\)
\(=>m-1\ne0\) ( Vì : \(\left(m-1\right)^2\ge0\forall x\) )
\(=>m\ne1\)
Theo Vi ét :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(3m-1\right)\left(1\right)\\x_1.x_2=12m-8\left(3\right)\end{matrix}\right.\)
Theo đề : \(x_1-2x_2=3\left(2\right)\)
Trừ vế theo vế (1) với (2) ta được :
\(3x_2=2\left(3m-1\right)-3=6m-5\\ =>x_2=\dfrac{6m-5}{3}\)
Thay vào (1) :
\(x_1+\dfrac{6m-5}{3}=2\left(3m-1\right)\)
\(=>x_1=6m-2-\dfrac{6m-5}{3}\)
\(=>x_1=\dfrac{18m-6-6m+5}{3}=\dfrac{12m-1}{3}\)
Thay giá trị x1 và x2 vào (3):
\(\dfrac{6m-5}{3}.\dfrac{12m-1}{3}=12m-8\)
\(=>\dfrac{\left(12m-1\right)\left(6m-5\right)}{9}=12m-8\\ =>72m^2-6m-60m+5=108m-72\\ =>72m^2-174m+77=0\\ =>\left[{}\begin{matrix}m_1=\dfrac{11}{6}\\m_2=\dfrac{7}{12}\end{matrix}\right.\left(TMDK\right)\)
Vậy \(m\in\left\{\dfrac{11}{6};\dfrac{7}{12}\right\}\) là 2 giá trị thỏa mãn đề
\(\Delta'=\left(3m-1\right)^2-\left(12m-8\right)=9\left(m-1\right)^2\)
Pt có 2 nghiệm pb khi \(9\left(m-1\right)^2>0\Rightarrow m\ne1\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(3m-1\right)\\x_1x_2=12m-8\end{matrix}\right.\)
Kết hợp với điều kiện đề bài ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(3m-1\right)\\x_1-2x_2=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x_2=2\left(3m-1\right)-3=6m-5\\x_1=2x_2+3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=\dfrac{6m-5}{3}\\x_1=\dfrac{12m-1}{3}\end{matrix}\right.\)
Thế vào \(x_1x_2=12m-8\)
\(\Rightarrow\left(\dfrac{6m-5}{3}\right)\left(\dfrac{12m-1}{3}\right)=12m-8\)
\(\Leftrightarrow72m^2-174m+77=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{11}{6}\\m=\dfrac{7}{12}\end{matrix}\right.\)

\(n^5+1⋮n^3+1\)
\(\Leftrightarrow n^5-n^3⋮n^3+1\)
\(\Leftrightarrow n^3\left(n^2-1\right)⋮n^3+1\)
Vì \(gcd\left(n^3,n^3+1\right)=1\) nên từ đây suy ra \(n^2-1⋮n^3+1\) (*)
Nếu \(n=1\) thì (*) thành \(0⋮2\) (thỏa mãn)
Nếu \(n\ge2\) thì (*) suy ra \(n^3+1\le n^2-1\)
\(\Leftrightarrow f\left(n\right)=n^3-n^2+2\le0\) (1)
Ta thấy \(f\left(n+1\right)-f\left(n\right)=\left(n+1\right)^3-\left(n+1\right)^2+2-n^3+n^2-2\)
\(=n^3+3n^2+3n+1-n^2-2n-1-n^3+n^2\)
\(=3n^2+n>0,\forall n\ge2\)
\(\Rightarrow f\left(n\right)\) là hàm số đồng biến trên \(ℕ_{\ge2}\) (cái này mình kí hiệu cho gọn thôi chứ bạn đừng viết vào bài làm nhé)
\(\Rightarrow f\left(n\right)\ge f\left(2\right)=6>0\)
Do đó (1) vô lý \(\Rightarrow n=1\) là giá trị duy nhất thỏa mãn ycbt.
\(\dfrac{n^5+1}{n^3+1}=\dfrac{\left(n+1\right)\left(n^4-n^3+n^2-n+1\right)}{\left(n+1\right)\left(n^2-n+1\right)}=\dfrac{n^4-n^3+n^2-n+1}{n^2-n+1}\)
\(=\dfrac{n^2\left(n^2-n+1\right)-\left(n-1\right)}{n^2-n+1}=n^2-\dfrac{n-1}{n^2-n+1}\)
Để \(n^5+1⋮n^3+1\Rightarrow\dfrac{n-1}{n^2-n+1}\in Z\)
- Với \(n=1\) thỏa mãn
- Với \(n>1\Rightarrow n^2-n>n^2-n=n\left(n-1\right)>n-1\)
\(\Rightarrow0< \dfrac{n-1}{n^2-n+1}< 1\) \(\Rightarrow\dfrac{n-1}{n^2-n+1}\notin Z\)
Vậy \(n=1\) là giá trị duy nhất thỏa mãn

\(\left\{{}\begin{matrix}4\sqrt{x+3}-9\sqrt{y+1}=2\\5\sqrt{x+3}+3\sqrt{y+1}=31\end{matrix}\right.\)
Đặt: \(\left\{{}\begin{matrix}\sqrt{x+3}=a>0\\\sqrt{y+1}=b>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4a-9b=2\\5a+3b=31\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a-9b=2\\15a+9b=93\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a-9b=2\\19a=95\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=5\end{matrix}\right.\left(tm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x+3}=5\\\sqrt{y+1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=22\\y=3\end{matrix}\right.\)
Vậy: ....

\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)

Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO
=>AD/AO=AH/AE
=>ΔADH đồng dạng với ΔAOE
=>góc ADH=góc AOE
=>góc DHO+góc DEO=180 độ
=>DEOH nội tiếp
=>góc EHO=góc EDO
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là đường trung trực của BC
=>OA vuông góc BC tại H
=>AH+AO=ABx2
Xet ΔABD và ΔAEB có
góc ABD = góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO
=>AD/AO=AH/AE
=>ΔADH đồng dạng với ΔAOE
=>góc ADH=góc AOE
=>góc DHO+góc DEO=180 độ
=>góc EHO=góc EDO
=>OB vuuong góc với d

Lời giải:
Theo định lý Bê-du về phép chia đa thức, số dư của $P(x)$ khi chia $2x-5$ là $P(\frac{5}{2})=\frac{5}{4}(\frac{5}{2})^3+\frac{5}{6}(\frac{5}{2})^2-\frac{21}{4}.\frac{5}{2}+\frac{1}{6}=\frac{377}{32}$
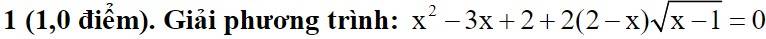
\(n\) chẵn \(\Rightarrow n=2k\left(k\inℤ\right)\)
Khi đó \(P=\dfrac{n}{12}+\dfrac{n^2}{8}+\dfrac{n^3}{24}\)
\(=\dfrac{k}{6}+\dfrac{k^2}{2}+\dfrac{k^3}{3}\)
\(=\dfrac{k+3k^2+2k^3}{6}\)
\(=\dfrac{k\left(2k^2+3k+1\right)}{6}\)
\(=\dfrac{k\left(2k+1\right)\left(k+1\right)}{6}\)
Nhận thấy \(k,k+1\) là 2 số nguyên liên tiếp nên \(k\left(k+1\right)\left(2k+1\right)⋮2\)
Nếu \(k\equiv0,2\left[3\right]\) thì dễ thấy \(k\left(2k+1\right)\left(k+1\right)⋮3\). Nếu \(k\equiv1\left[3\right]\) thì \(2k+1\equiv2.1+1=3\left[3\right]\) nên \(k\left(2k+1\right)\left(k+1\right)⋮3\).
Do vậy, \(k\left(k+1\right)\left(2k+1\right)⋮6\). Suy ra đpcm.
Giải thích các bước giải:
A=n12+n28+n324�=�12+�28+�324
=2n+3n2+n324=2�+3�2+�324
=n(n2+3n+2)24=�(�2+3�+2)24
=n24⋅(n2+3n+2)=�24⋅(�2+3�+2)
=n24[n(n+1)+2(n+1)]=�24[�(�+1)+2(�+1)]
=n(n+1)(n+2)24=�(�+1)(�+2)24
Vì n(n+1)(n+2)�(�+1)(�+2) là tích ba số nguyên liên tiếp nên chia hết cho 33
Lại có n� là số chẵn, nên đặt n=2k�=2�, ta có:
n(n+1)(n+2)=2k(2k+1)(2k+2)=4k(k+1)(2k+1)�(�+1)(�+2)=2�(2�+1)(2�+2)=4�(�+1)(2�+1)
Do k(k+1)�(�+1) là tích hai số nguyên liên tiếp nên chia hết cho 2 và 4k(k+1)(2k+1)4�(�+1)(2�+1) chia hết cho 8
Vậy A chia hết cho 3 và 8, vậy A chia hết cho 24
⇒A⇒� là số nguyên